本节内容参照小土堆的
pytorch
入门视频教程,主要通过查询文档的方式讲解如何搭建卷积神经网络。学习时要学会查询文档,这样会比直接搜索良莠不齐的博客更快、更可靠。讲解的内容主要是
pytorch
核心包中
TORCH.NN
中的内容(
nn
是
Neural Netwark
的缩写)。

通常,我们定义的神经网络模型会继承
torch.nn.Module
类,该类为我们定义好了神经网络骨架。

卷积层
对于图像处理来说,我们通常使用二维卷积,即使用
torch.nn.Conv2d
类:

创建该类时,我们通常只需要传入以下几个参数,其他不常用参数入门时可以不做了解,使用默认值即可,以后需要时再查询文档:
in_channels (int):输入数据的通道数,图片通常为3out_channels (int):输出数据的通道数,也是卷积核的个数kernel_size (int or tuple):卷积核大小,传入int表示正方形,传入tuple代表高和宽stride (int or tuple, optional):卷积操作的步长,传入int代表横向和纵向步长相同,默认为1padding (int, tuple or str, optional):填充厚度,传入int代表上下左右四个边填充厚度相同,默认为0,即不填充padding_mode (string, optional):填充模式,默认为\'zeros\',即0填充
卷积操作后输出的张量的高和宽计算公式如下:

其中
input
和
output
中的
N
代表
BatchSize
,
C
代表通道数,他们不影响
H
和
W
的计算。在保持
dilation
为默认值
1
的情况下,计算公式可简化为如下:
H_{out} = \\left\\lfloor\\frac{H_{in} + 2 \\times \\text{padding}[0] -\\text{kernel\\_size}[0]}{\\text{stride}[0]} + 1\\right\\rfloorW_{out} = \\left\\lfloor\\frac{W_{in} + 2 \\times \\text{padding}[1] – \\text{kernel\\_size}[1]}{\\text{stride}[1]} + 1\\right\\rfloor
池化层
常用的二维最大池化定义在
torch.nn.MaxPool2d
类中:

创建该类时,我们通常只需要传入以下几个参数,其他不常用参数入门时可以不做了解,使用默认值即可,以后需要时再查询文档:
kernel_size:池化操作时的窗口大小stride:池化操作时的步长,默认为kernel_sizepadding:每个边的填充厚度(0填充)
池化操作后输出的张量的高和宽计算公式与卷积操作后的计算公式相同。
非线性激活
常见的
ReLU
激活定义在
torch.nn.ReLU
类中:

参数
inplace
代表是否将
ouput
直接修改在
input
中。
线性层
线性层的定义在
torch.nn.Linear
类中:

创建线性层使用的参数如下:
in_features:输入特征大小out_features:输出特征大小bias:是否添加偏置,默认为True
模型搭建示例
下图是一个
CIFAR10
数据集上的分类模型,下面将根据图片进行模型代码的编写。

1.由于
CIFAR10
数据集中图片为
3*32*32
,所以图中模型的输入为3通道,高宽都为32的张量。
2.使用
5*5
的卷积核进行卷积操作,得到通道数为
32
,高和宽为
32
的张量。因此我们可以推出该卷积层的参数如下:
in_channels = 3out_channels = 32kernel_size = 5stride = 1padding = 2
注:将 Hin = 32,Hout = 32 以及
kernal_size[0] = 5
三个参数带入:
H_{out} = \\left\\lfloor\\frac{H_{in} + 2 \\times \\text{padding}[0] -\\text{kernel\\_size}[0]}{\\text{stride}[0]} + 1\\right\\rfloor
有:
32 = \\left\\lfloor\\frac{32 + 2 \\times \\text{padding}[0] -\\text{5}}{\\text{stride}[0]} + 1\\right\\rfloor
发现
stride[0] = 1
和
padding[0] = 2
可以使得等式成立。同理可以得到
stride[1] = 1
和
padding[1] = 2
。
3.使用
2*2
的核进行最大池化操作,得到通道数为
32
,高和宽为
16
的张量。可以推出该池化层的参数如下:
kernel_size = 2stride = 2padding = 0
注:
stride
和
padding
推导方式与2中相同。
4.使用
5*5
的卷积核进行卷积操作,得到通道数为
32
,高和宽为
16
的张量。因此我们可以推出该卷积层的参数如下:
in_channels = 32out_channels = 32kernel_size = 5stride = 1padding = 2
5.使用
2*2
的核进行最大池化操作,得到通道数为
32
,高和宽为
8
的张量。可以推出该池化层的参数如下:
kernel_size = 2stride = 2padding = 0
6.使用
5*5
的卷积核进行卷积操作,得到通道数为
64
,高和宽为
8
的张量。因此我们可以推出该卷积层的参数如下:
in_channels = 32out_channels = 64kernel_size = 5stride = 1padding = 2
7.使用
2*2
的核进行最大池化操作,得到通道数为
64
,高和宽为
4
的张量。可以推出该池化层的参数如下:
kernel_size = 2stride = 2padding = 0
8.将
64*4*4
的张量进行展平操作得到长为
1024
的向量。
9.将长为
1024
的向量进行线性变换得到长为
64
的向量(隐藏层),可以推出该线性层的参数如下:
in_features:1024out_features:64
10.将长为
64
的向量进行线性变换得到长为
10
的向量,可以推出该线性层的参数如下:
in_features:64out_features:10
因此,模型代码如下:
from torch import nnclass MyModel(nn.Module):def __init__(self):super(MyModel, self).__init__()self.conv1 = nn.Conv2d(3, 32, 5, padding=2)self.max_pool1 = nn.MaxPool2d(2)self.conv2 = nn.Conv2d(32, 32, 5, padding=2)self.max_pool2 = nn.MaxPool2d(2)self.conv3 = nn.Conv2d(32, 64, 5, padding=2)self.max_pool3 = nn.MaxPool2d(2)self.flatten = nn.Flatten()self.linear1 = nn.Linear(1024, 64)self.linear2 = nn.Linear(64, 10)# 必须覆盖该方法,该方法会在实例像函数一样调用时被调用,后面会有示例def forward(self, x):x = self.conv1(x)x = self.max_pool1(x)x = self.conv2(x)x = self.max_pool2(x)x = self.conv3(x)x = self.max_pool3(x)x = self.flatten(x)x = self.linear1(x)x = self.linear2(x)return x
sequential
使用
torch.nn.sequential
可以简化模型的搭建代码,他是一个顺序存放
Module
的容器。当
sequential
执行时,会按照
Module
在构造函数中的先后顺序依次调用,前面
Module
的输出会作为后面
Module
的输入。
使用
sequential
,上一节的代码可以简化为:
from torch import nnclass MyModel(nn.Module):def __init__(self):super.__init__(MyModel, self)self.model = nn.Sequential(nn.Conv2d(3, 32, 5, padding=2),nn.MaxPool2d(2),nn.Conv2d(32, 32, 5, padding=2),nn.MaxPool2d(2),nn.Conv2d(32, 64, 5, padding=2),nn.MaxPool2d(2),nn.Flatten(),nn.Linear(1024, 64),nn.Linear(64, 10))def forward(self, x):x = self.model(x)return x
损失函数、反向传播以及优化器
上面两节我们已经将
CIFAR10
的分类模型搭建好,但还需要进行训练后才能用来预测分类。训练模型时,会用损失函数来衡量模型的好坏,并利用反向传播来求梯度,然后利用优化器对模型参数进行梯度下降,多次循环往复以训练出最优的模型。
模型训练代码如下:
import torchfrom torch.optim import SGDimport torchvisionfrom torch.utils.data import DataLoaderfrom cifar10_model import MyModelfrom torch import nnfrom torch.utils import tensorboarddef train():# 获取 cifar10 数据集root = "./dataset"transform = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])train_cifar10 = torchvision.datasets.CIFAR10(root=root, train=True,transform=transform,download=True)# 创建dataloadertrain_dataloader = DataLoader(dataset=train_cifar10, batch_size=64,shuffle=True,num_workers=16)# 创建模型model = MyModel()# 创建交叉熵损失函数loss = nn.CrossEntropyLoss()# 创建优化器,传入需要更新的参数,以及学习率optim = SGD(model.parameters(), lr=0.01)# 创建 SummaryWriterwriter = tensorboard.SummaryWriter("logs")# 写入模型图,随机生成一个输入writer.add_graph(model, torch.randn(64, 3, 32, 32))for epoch in range(20):loss_temp = 0.0for batch_num, batch_data in enumerate(train_dataloader):images, targets = batch_data# 像调用方法一样调用实例outputs = model(images)loss_res = loss(outputs, targets)loss_temp = loss_res# 清空前一次计算的梯度optim.zero_grad()# 反向传播求梯度loss_res.backward()# 更新参数optim.step()# 记录每个epoch之后的losswriter.add_scalar("Loss/train", loss_temp, epoch)writer.close()if __name__ == "__main__":train()
模型图如下:
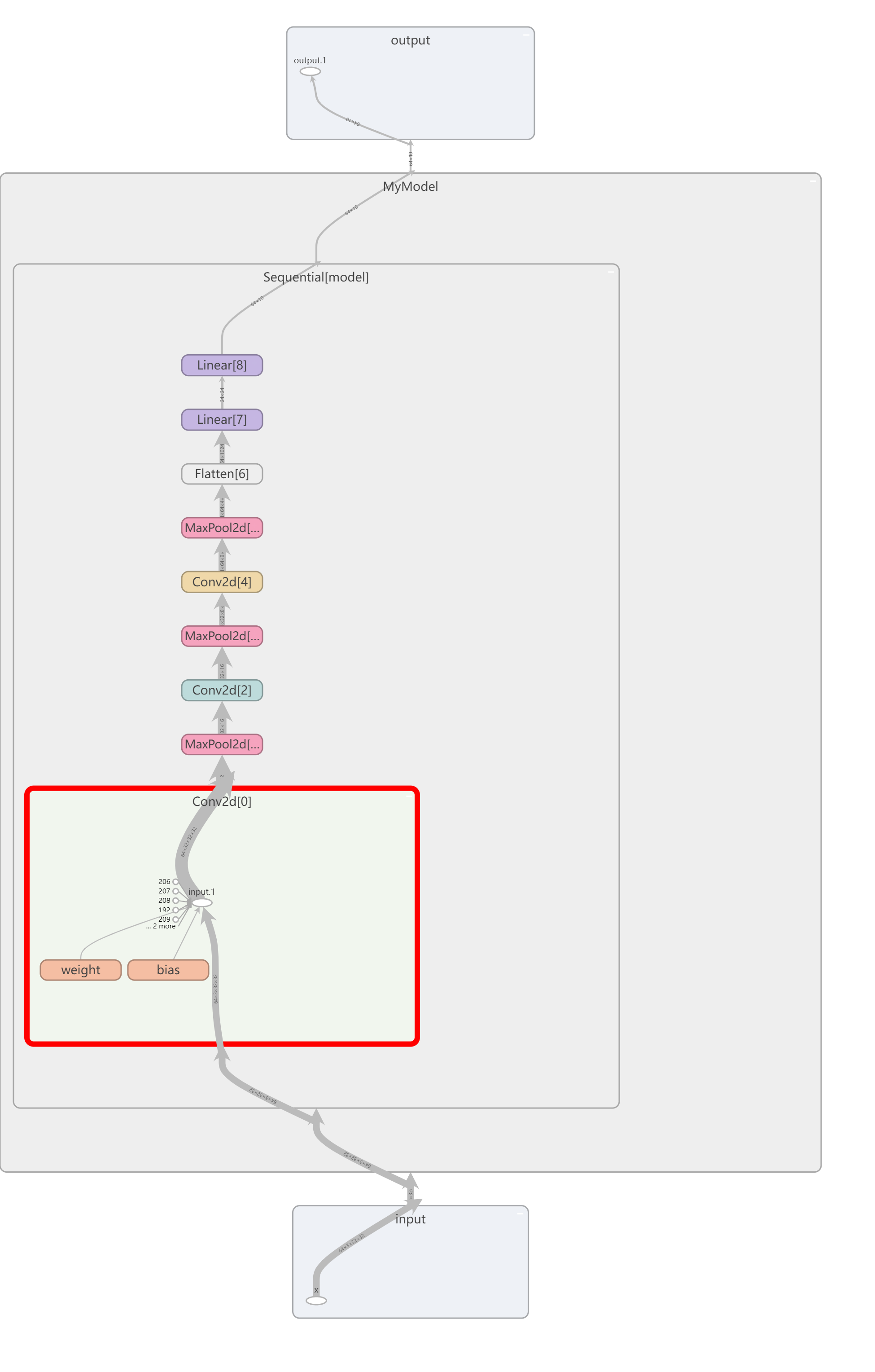
损失函数随训练周期的下降情况如下:

 爱站程序员基地
爱站程序员基地


