目录

• 1. 符号定义
• 2. 隐藏层到输出层的权重更新
• 3. 输出层神经元阈值更新
• 4. 输入层到隐藏层的权重更新
• 5. 隐藏层神经元阈值更新

1. 符号定义

• 本文以单隐藏层的神经网络结构，均方误差为损失函数为例来详细推导各个参数的梯度更新。
• 给定训练集D={(x1,y1),(x2,y2),…,(xm,ym)},xi∈Rd,yi∈RlD=\\left\\{\\bm{(x_1, y_1), (x_2, y_2),…,(x_m, y_m)}\\right\\}, \\bm{x}_i\\in \\Bbb R^d, \\bm y_i \\in \\Bbb R^lD={(x1​,y1​),(x2​,y2​),…,(xm​,ym​)},xi​∈Rd,yi​∈Rl, 即输入示例由ddd个属性描述，输出lll维实值向量。为便于讨论图1给出了一个拥有ddd个输入神经元、lll个输出神经元、qqq个隐层神经元的多层前馈网络结构，其中输出层第jjj个神经元的阀值用θj\\theta_jθj​表示，隐层第hhh个神经元的阔值用γh\\gamma_hγh​ 表示。输入层第iii个神经元与隐居第hhh个神经元之间的连接权为vihv_{ih}vih​，隐层第hhh个神经元与输出层第jjj个神经元之间的连接权为whjw_{hj}whj​。
• 记隐层第hhh个神经元接收到的输入为αh=∑i=1dvihxi\\alpha_h= \\sum_{i=1}^d v_{ih} x_iαh​=∑i=1d​vih​xi​，输出层第jjj个神经元接收到的输入为β=∑h=1qwhjbh\\beta=\\sum_{h=1}^q w_{hj} b_hβ=∑h=1q​whj​bh​，其中bhb_hbh​为隐层第hhh个神经元的输出。假设隐层和输出层神经元都使用SigmoidSigmoidSigmoid函数f(x)=11+e−xf(x)=\\frac{1}{1+e^{-x}}f(x)=1+e−x1​。
• 对训练例(xk,yk)\\bm{(x_k, y_k)}(xk​,yk​)，假定神经网络的输出为y^k=(y^1k,y^2k,…,y^lk)\\bm{\\hat y}_k=(\\hat y_{1}^k, \\hat y_{2}^k,…,\\hat y_{l}^k)y^​k​=(y^​1k​,y^​2k​,…,y^​lk​)，即
  y^jk=f(βj−θj)(1)\\hat y_{j}^k=f(\\beta_j-\\theta_j) \\tag{1}y^​jk​=f(βj​−θj​)(1)
  网络在(xk,yk)\\bm{(x_k, y_k)}(xk​,yk​)上的均分误差为
  Ek=12∑j=1l(y^jk−yjk)2(2)E_k=\\frac{1}{2} \\sum_{j=1}^l {(\\hat y_{j}^k-y_{j}^k) \\tag{2}}^2Ek​=21​j=1∑l​(y^​jk​−yjk​)2(2)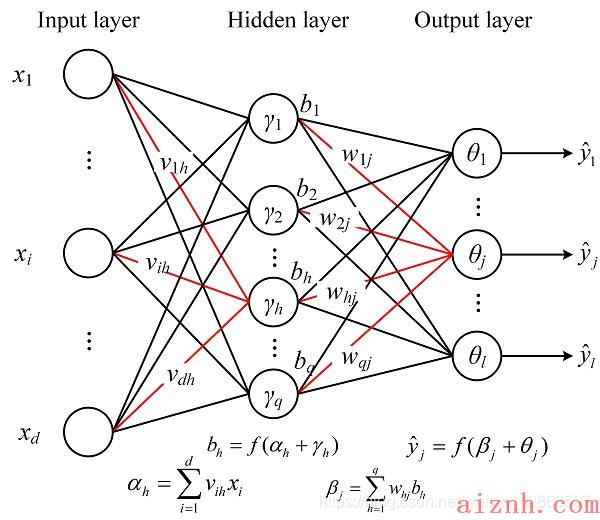
  
  图1 BP 络及算法中的交量符号
  BP算法基于梯度下降（gradient descent）策略，以目标的负梯度方向对参数进行更新。任意参数vvv的更新估计式为
  v←v+Δvv \\leftarrow v+ \\Delta vv←v+Δv

2. 隐藏层到输出层的权重更新

本节对图1中的隐层到输出层的连接权重whjw_{hj}whj​的更新进行推导。
对公式(1)的误差EkE_kEk​，给定学习速率η\\etaη，有权重whjw_{hj}whj​的更新公式为
Δwhj=−η∂Ek∂whj(3)\\Delta w_{hj}=-\\eta \\frac{\\partial E_k}{\\partial w_{hj}} \\tag{3}Δwhj​=−η∂whj​∂Ek​​(3)
根据图1可知，whjw_{hj}whj​先影响到第jjj个输出层神经元的输入值βj\\beta_jβj​，然后βj\\beta_jβj​再影响到该神经元的输出值y^jk\\hat y_{j}^ky^​jk​，最后y^jk\\hat y_{j}^ky^​jk​影响到EkE_kEk​，因此EkE_kEk​对whjw_{hj}whj​的偏导数可改写为
∂Ek∂whj=∂Ek∂y^jk⋅∂y^jk∂βj⋅∂βj∂whj(4)\\frac {\\partial E_k}{\\partial w_{hj}}=\\frac{\\partial E_k}{\\partial \\hat y_{j}^k} \\cdot \\frac{\\partial \\hat y_{j}^k}{\\partial \\beta_j} \\cdot \\frac{\\partial \\beta_j}{\\partial w_{hj}} \\tag{4}∂whj​∂Ek​​=∂y^​jk​∂Ek​​⋅∂βj​∂y^​jk​​⋅∂whj​∂βj​​(4)
根据βj\\beta_jβj​的定义，显然有
∂βj∂whj=∂whj(∑h=1qwhjbh)=bh(5)\\frac {\\partial \\beta_j}{\\partial w_{hj}}=\\frac{\\partial}{w_{hj}} (\\sum_{h=1}^q w_{hj} b_h)=b_h \\tag{5}∂whj​∂βj​​=whj​∂​(h=1∑q​whj​bh​)=bh​(5)
由于SigmoidSigmoidSigmoid函数有一个很好的性质：
f′(x)=f(x)(1−f(x))(6)f^{\\prime}(x)=f(x)(1-f(x)) \\tag{6}f′(x)=f(x)(1−f(x))(6)
因此根据公式(1)和(2)，有
gj=−∂Ek∂y^jk⋅∂y^jk∂βj=−(y^jk−yjk)f′(βj−θj)=−(y^jk−yjk)y^jk(1−y^jk)=y^jk(1−y^jk)(yjk−y^jk)(7) \\begin{aligned}g_j&= – \\frac{\\partial E_k}{\\partial \\hat y_j^k} \\cdot \\frac{\\partial \\hat y_j^k}{\\partial \\beta_j} \\\\&=-(\\hat y_j^k-y_j^k) f^{\\prime} (\\beta_j-\\theta_j)\\\\&=-(\\hat y_j^k-y_j^k) \\hat y_j^k (1-\\hat y_j^k)\\\\&=\\hat y_j^k (1-\\hat y_j^k) (y_j^k-\\hat y_j^k) \\tag{7} \\end{aligned}gj​​=−∂y^​jk​∂Ek​​⋅∂βj​∂y^​jk​​=−(y^​jk​−yjk​)f′(βj​−θj​)=−(y^​jk​−yjk​)y^​jk​(1−y^​jk​)=y^​jk​(1−y^​jk​)(yjk​−y^​jk​)​(7)

将公式(5)和(7)带入公式(4)，再带入公式(3)，就得到了BP算法中关于权重whjw_{hj}whj​的更新公式
Δwhj=ηgjbh(8)\\Delta w_{hj}=\\eta g_j b_h \\tag{8}Δwhj​=ηgj​bh​(8)

3. 输出层神经元阈值更新

对于输出层第jjj个神经元的阈值θj\\theta_jθj​，它首先影响到该神经元的输出值y^jk\\hat y_j^ky^​jk​，再影响到EkE_kEk​，因此有
Δθj=−η∂Ek∂θj=−η∂Ek∂y^jk⋅∂y^jk∂θj=−η(y^jk−yjk)f′(βj−θj)=−η(y^jk−yjk)[−y^jk(1−y^jk)]=−η[y^jk(1−y^jk)(yjk−y^jk)=−ηgj(9) \\begin{aligned}\\Delta \\theta_j&=-\\eta \\frac{\\partial E_k}{\\partial \\theta_j}\\\\&=-\\eta \\frac{\\partial E_k}{\\partial \\hat y_j^k} \\cdot \\frac{\\partial \\hat y_j^k}{\\partial \\theta_j}\\\\&=-\\eta (\\hat y_j^k-y_j^k) f^{\\prime} (\\beta_j-\\theta_j)\\\\&=-\\eta (\\hat y_j^k – y_j^k) [-\\hat y_j^k (1-\\hat y_j^k)]\\\\&=-\\eta[\\hat y_j^k (1-\\hat y_j^k) (y_j^k-\\hat y_j^k) \\\\&=-\\eta g_j \\tag{9} \\end{aligned}Δθj​​=−η∂θj​∂Ek​​=−η∂y^​jk​∂Ek​​⋅∂θj​∂y^​jk​​=−η(y^​jk​−yjk​)f′(βj​−θj​)=−η(y^​jk​−yjk​)[−y^​jk​(1−y^​jk​)]=−η[y^​jk​(1−y^​jk​)(yjk​−y^​jk​)=−ηgj​​(9)

4. 输入层到隐藏层的权重更新

对于输入层的第iii个神经元到隐藏层的第hhh个神经元的权重值vihv_{ih}vih​，它首先影响到隐藏层第hhh个神经元的输入值αh\\alpha_hαh​，然后αh\\alpha_hαh​再影响到第hhh个神经元的输出值bhb_hbh​，最后bhb_hbh​再影响到EkE_kEk​。以下推导EkE_kEk​对vihv_{ih}vih​的偏导数：
∂Ek∂vih=∂Ek∂bh⋅∂bh∂αh⋅∂αh∂vih(10)\\frac {\\partial E_k}{\\partial v_{ih}} = \\frac{\\partial E_k}{\\partial b_h} \\cdot \\frac{\\partial b_h}{\\partial \\alpha_h} \\cdot \\frac{\\partial \\alpha_h}{\\partial v_{ih}} \\tag{10}∂vih​∂Ek​​=∂bh​∂Ek​​⋅∂αh​∂bh​​⋅∂vih​∂αh​​(10)
首先考虑第三项：
∂αh∂vih=xi(11)\\frac {\\partial \\alpha_h}{\\partial v_{ih}}=x_i \\tag{11}∂vih​∂αh​​=xi​(11)
其次考虑第一项和第二项的乘积，如公式(12)所示，先考虑第二项的导数结果：
∂Ek∂bh⋅∂bh∂αh=∂Ek∂bh⋅f′(αh+γh)=∂Ek∂bh⋅bh(1−bh)(12) \\begin{aligned}& \\frac{\\partial E_k}{\\partial b_h} \\cdot \\frac{\\partial b_h}{\\partial \\alpha_h}\\\\&=\\frac{\\partial E_k}{\\partial b_h} \\cdot f^{\\prime}(\\alpha_h+\\gamma_h)\\\\&= \\frac{\\partial E_k}{\\partial b_h} \\cdot b_h(1-b_h) \\tag{12} \\end{aligned}​∂bh​∂Ek​​⋅∂αh​∂bh​​=∂bh​∂Ek​​⋅f′(αh​+γh​)=∂bh​∂Ek​​⋅bh​(1−bh​)​(12)

下面考虑EkE_kEk​对bhb_hbh​的偏导数，据图1可知bhb_hbh​先影响到βj\\beta_jβj​，然后βj\\beta_jβj​影响到y^jk\\hat y_j^ky^​jk​。由于βj=∑h=1qwhjbh=w1jb1+…+whjbh+…+wqjbq\\beta_j=\\sum_{h=1}^q w_{hj} b_h=w_{1j}b_1+…+w_{hj}b_h+…+w_{qj}b_qβj​=∑h=1q​whj​bh​=w1j​b1​+…+whj​bh​+…+wqj​bq​，因此bh(h=1,…,q)b_h (h=1,…,q)bh​(h=1,…,q)会对所有的βj(j=1,…,l)\\beta_j (j=1,…,l)βj​(j=1,…,l)产生影响，需对所有的βj\\beta_jβj​求和：

∂Ek∂bh=∑j=1l∂Ek∂βj⋅∂βj∂bh=∑j=1l(∂Ek∂y^jk⋅∂y^jk∂βj)⋅whj=−∑j=1lgjwhj(13) \\begin{aligned}\\frac {\\partial E_k}{\\partial b_h}&=\\sum_{j=1}^l \\frac{\\partial E_k}{\\partial \\beta_j} \\cdot \\frac{\\partial \\beta_j}{\\partial b_h}\\\\&=\\sum_{j=1}^l (\\frac{\\partial E_k}{\\partial \\hat y_j^k} \\cdot \\frac{\\partial \\hat y_j^k}{\\partial \\beta_j} ) \\cdot w_{hj} \\\\&=-\\sum_{j=1}^l g_j w_{hj} \\tag{13}\\end{aligned}∂bh​∂Ek​​​=j=1∑l​∂βj​∂Ek​​⋅∂bh​∂βj​​=j=1∑l​(∂y^​jk​∂Ek​​⋅∂βj​∂y^​jk​​)⋅whj​=−j=1∑l​gj​whj​​(13)

将公式(13)带入(12)中有
∂Ek∂bh⋅∂bh∂αh=−bh(1−bh)⋅∑j=1lgjwhj(14) \\frac{\\partial E_k}{\\partial b_h} \\cdot \\frac{\\partial b_h}{\\partial \\alpha_h}= -b_h(1-b_h) \\cdot \\sum_{j=1}^l g_j w_{hj} \\tag{14}∂bh​∂Ek​​⋅∂αh​∂bh​​=−bh​(1−bh​)⋅j=1∑l​gj​whj​(14)
令
eh=−∂Ek∂bh⋅∂bh∂αh=bh(1−bh)⋅∑j=1lgjwhj(15)e_h=- \\frac{\\partial E_k}{\\partial b_h} \\cdot \\frac{\\partial b_h}{\\partial \\alpha_h}=b_h(1-b_h) \\cdot \\sum_{j=1}^l g_j w_{hj} \\tag{15}eh​=−∂bh​∂Ek​​⋅∂αh​∂bh​​=bh​(1−bh​)⋅j=1∑l​gj​whj​(15)

将公式(15)和公式(11)带入公式(10)中有
∂Ek∂vih=ehxi(16)\\frac {\\partial E_k}{\\partial v_{ih}} = e_h x_i \\tag{16}∂vih​∂Ek​​=eh​xi​(16)
进一步可得
Δvih=ηehxi(17)\\Delta v_{ih}=\\eta e_h x_i \\tag{17}Δvih​=ηeh​xi​(17)

5. 隐藏层神经元阈值更新

对于隐藏层第hhh个神经元的阈值γh\\gamma_hγh​, 它首先影响到
∂Ek∂γh=∂Ek∂bh⋅∂bh∂γh=∂Ek∂bh⋅f′(αh+γh)=∂Ek∂bh⋅bh(1−bh)(18) \\begin{aligned}\\frac {\\partial E_k}{\\partial \\gamma_h}&=\\frac {\\partial E_k}{\\partial b_h} \\cdot \\frac{\\partial b_h}{\\partial \\gamma_h}\\\\&=\\frac {\\partial E_k}{\\partial b_h} \\cdot f^{\\prime}(\\alpha_h + \\gamma_h)\\\\&=\\frac {\\partial E_k}{\\partial b_h} \\cdot b_h(1-b_h) \\tag{18}\\end{aligned}∂γh​∂Ek​​​=∂bh​∂Ek​​⋅∂γh​∂bh​​=∂bh​∂Ek​​⋅f′(αh​+γh​)=∂bh​∂Ek​​⋅bh​(1−bh​)​(18)

将公式(13)带入(18)有
∂Ek∂γh=−bh(1−bh)⋅∑j=1lgjwhj=−eh(19)\\frac {\\partial E_k}{\\partial \\gamma_h}=-b_h(1-b_h) \\cdot \\sum_{j=1}^l g_j w_{hj} = -e_h \\tag{19} ∂γh​∂Ek​​=−bh​(1−bh​)⋅j=1∑l​gj​whj​=−eh​(19)
因此有
Δγh=−η∂Ek∂γh=ηeh(20)\\Delta \\gamma_h=-\\eta \\frac {\\partial E_k}{\\partial \\gamma_h}=\\eta e_h \\tag{20}Δγh​=−η∂γh​∂Ek​​=ηeh​(20)

参考资料：
周志华《机器学习》5.3节BP神经网络内容