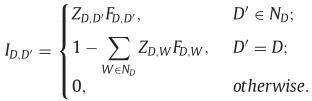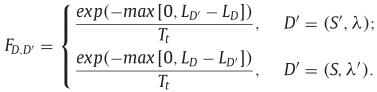Maximizing influence under influence loss constraint in social networks

在影响力损失约束下的社交网络中的最大化影响

一、概述

1.摘要

• 常规的影响最大化问题：从社交网络中选取K个节点，在网络上拥有最大的影响力（能够传播最多的节点）。
• 问题：先前对选取前K个影响节点的研究，是假设所有选定的K个节点都可以按预期传播影响。但是某些选定的节点在实践中可能无法正常运行，我们希望选择K个节点，即使在一部分节点故障后，造成的损失达到我们所能接受的地步。
• 本文问题的目标：找到 top-K 个影响节点，它的一个子集R(R<K)由于发生故障而造成的影响损失达到阈值。
• 算法：一种基于约束的模拟退火方法（CAS）。

2.说明

图1

• v1只能由v2激活，概率为0.3。对于节点v3，两条路径，v2->v1->v3和v2->v3，此网络中集合{v2,v5,v7}可以传播影响。v3可能会受到其中一个或者两个的影响，因此它受到的影响为：1-(1–0.6) × (1–0.3 × 0.7) = 0.684。相似的，v4：1-(1–0.4) × (1–0.3 × 0.6) ×(1–0.1) = 0.5572。v6的1-(1–0.2)×(1–0.2) = 0.36。{v2,v5,v7}有确定的影响（=1）。因此，由{v2,v5,v7}造成的影响为：0.3 + 0.684 + 0.5572 + 0.36 + 3 = 4.9012。
• 对于一个小规模的网络，我们可以直接计算每三个节点集的影响，并确定节点集{v2,v5,v7}表现出最大的影响力(影响值= 4.9012)，而节点{v1,v2,v5}是次优的影响力(影响值= 4.864)。假设在选定集中只有一个节点发生故障。然后，我们计算集合中剩余的两个节点所表现出的影响。当节点v2发生故障时，第一组的最大损失为2.4412（4.9012-（0*3+0.1+1+1+0.36））。而当第二组中v1发生故障时，最大损失为1.2264 (???我算的是1.604) 。给定影响损失的阈值为1.5，我们能接受第二组节点{v1,v2,v5}的故障损失，但此时它们不是常规影响最大化问题中影响力最大的3个节点。

二、问题公式化

1.条件

  有向图G={υ\\upsilonυ,ε\\varepsilonε}，|υ\\upsilonυ|=N个点，|ε\\varepsilonε|=M条边。对于每条边(v,u)∈ε\\varepsilonε,Pvu是影响此边的传播概率\\color{red}{P_{vu}是影响此边的传播概率}Pvu​是影响此边的传播概率。

2.常规的影响最大化问题

  常规的影响最大化问题是找到种子集S⊆V,并且给定|S|=K，从而根据扩散模型将影响σ(S)最大化。给定一个初始集合S，我们使用独立级联模型（IC）传播影响。Zt是在t时被激活的节点集\\color{red}{Z_t是在t时被激活的节点集}Zt​是在t时被激活的节点集，并且Z0=S。每个激活的节点v(∈Zt)仅有一次机会去激活任意非激活态的邻居节点，u∈∪0tZtu\\in\\cup_0^tZ_tu∈∪0t​Zt​，激活的概率为Pvu。当且仅当我们找不到任何可以被激活的节点时，传播过程才会终止。所有活动节点的预期数量表示为：σ(S)=∑0∞∣Zt∣\\sigma(S)=\\sum_0^{\\infty}|Z_t|σ(S)=∑0∞​∣Zt​∣

3.影响力损失约束下的影响最大化问题

  在影响传播的过程中，A是激活失败（故障）的集合，大小为R(=∣A∣)\\color{red}{A是激活失败（故障）的集合，大小为R(=|A|)}A是激活失败（故障）的集合，大小为R(=∣A∣)。网络中的任何节点都可能发生故障，但是种子集S中的节点发生故障时，导致的影响损失将会更大。

• TR为发生故障的节点总数，R为发生故障的节点是种子节点的数量\\color{red}{TR为发生故障的节点总数，R为发生故障的节点是种子节点的数量}TR为发生故障的节点总数，R为发生故障的节点是种子节点的数量。
• Ratio=Ave[σ(S−A)]σ(S)\\color{red}{Ratio=\\frac{Ave[\\sigma(S-A)]}{\\sigma(S)}}Ratio=σ(S)Ave[σ(S−A)]​ 表示不包括故障节点时种子集合的平均预期影响÷种子集合的影响。

  本文中将故障节点集视为种子集合的子集，A⊆S，其中R≤K。本文中将影响损失定义为减少的影响力[σ(S)−σ(S−A)]。因为R（故障节点集）由于故障而要从网络中删除，故从本质上来说我们需要计算(K-R)节点的影响。我们考虑到最坏的情况，最大损失MaxLoss，发生在(K-R)剩余节点的最大影响与（K-R）中∀\\forall∀节点的影响相比是最小的情况下。形式化的来讲：∣A∣=R，MaxLoss=σ(S)−minA⊆Sσ(S−A)|A|=R，MaxLoss=σ(S)-min_{A⊆S}σ(S−A)∣A∣=R，MaxLoss=σ(S)−minA⊆S​σ(S−A)。
  ★★★\\bigstar\\bigstar\\bigstar★★★对于给定的社交网络，我们的问题是找到大小为K的种子集S，使得此时的σ(S)最大，约束条件是由于大小为R的失败集A，最大损失不超过阈值η(>0)。我们可以将具有影响损失约束(IMIL)的影响最大化问题使用公式1将其定义为约束优化问题：
Given: G,K,R, η\\etaη
Objective: maxS⊆V,∣S∣=Kσ(S)\\underset{S\\subseteq V,|S|=K}{max} \\sigma(S)S⊆V,∣S∣=Kmax​σ(S)
Constraint: σ(S)−minA⊆S,∣A∣=Rσ(S−A)≤η\\sigma(S)-\\underset{A\\subseteq S,|A|=R}{min}\\sigma(S-A)\\leq\\etaσ(S)−A⊆S,∣A∣=Rmin​σ(S−A)≤η

公式1**注意：**

• IMIL:influence maximization problem with influence loss constraint.
• IM:influence maximization problem.
• 当η\\etaη足够大时，IMIL问题则就变为了常规的影响最大化问题。
• 将IMLL问题归约为IM问题，因为IM问题是NP-Hard，则IMIL问题是HP-Hard。

三、基于CSA的算法

1.CSA算法

由公式1得max[0,σ(S)−minA⊆S(S−A)−η]=0max[0,\\sigma(S)-min_{A\\subseteq S}(S-A)-\\eta]=0max[0,σ(S)−minA⊆S​(S−A)−η]=0 其中MaxLoss≤ηMaxLoss\\leq\\etaMaxLoss≤η
惩罚函数为：
LΩ(S,λ)=−σ(S)+λ×max[0,σ(S)−minσ(S−A)−η]L_\\Omega(S,\\lambda)=-\\sigma(S)+\\lambda\\times max[0,\\sigma(S)-min\\ \\sigma(S-A)-\\eta]LΩ​(S,λ)=−σ(S)+λ×max[0,σ(S)−minσ(S−A)−η]
Ω\\OmegaΩ是种子集S和惩罚因子λ\\lambdaλ的联合空间。D=(S,λ)⊆ΩD=(S,\\lambda)\\subseteq\\OmegaD=(S,λ)⊆Ω是一个解。
算法：

图3：CSA算法

解释：

1. 初始化D和温度T0。
2. 计算惩罚值LD（第4行）。
3. 计算搜索空间中当前解空间D邻居的惩罚函数（5、6行）。
   3.1 ND可通过列出S的相邻节点和λ的相邻值生成。
   3.2 从ND中随机选择一个新解D’。
   3.3 计算惩罚函数的差异，ΔL=LD′−LD\\Delta_L=L_{D~\’}-L_{D}ΔL​=LD′​−LD​
4. 9-23行检查是否接受新的解决方案。如果λ\\lambdaλ不变的话，接受惩罚值较低的新解（此时MaxLoss≤ηMaxLoss\\leq\\etaMaxLoss≤η），从而返回较大的σ(S)\\sigma(S)σ(S)。
   4.1 我们仅接受概率exp(−ΔLTt)exp(-\\frac{\\Delta_L}{T_t})exp(−Tt​ΔL​​)随时间的推移而降低的具有较大惩罚值的解决方案（10-15行）。
5. 相反(λ\\lambdaλ发生改变)，如果种子集合S不更新，接受具有较大惩罚值的新解（17-23行）。
6. 在温度Tt 时搜索q次后，我们计算出一个新的温度（稍后解释）并进入下一轮迭代（25-26行）。当达到终止温度Tf 时，终止CSA。

2.相关参数

• λ\\lambdaλ的离散空间为：Λ(λ)=[0,maxσ(S)10%K∗(N−K),maxσ(S)20%K∗(N−K),…,maxσ(S)]\\Lambda(\\lambda)=[0,\\frac{max\\ \\sigma(S)}{10\\%K*(N-K)},\\frac{max\\ \\sigma(S)}{20\\%K*(N-K)},…,max\\ \\sigma(S)]Λ(λ)=[0,10%K∗(N−K)maxσ(S)​,20%K∗(N−K)maxσ(S)​,…,maxσ(S)]
• ρ=2maxσ(S)(1+maxσ(A))\\rho=2max\\ \\sigma(S)(1+max\\ \\sigma(A))ρ=2maxσ(S)(1+maxσ(A))是Tt的一个因子。（推导见注释2）
• 使用广义的ISP方法估算影响力。ISP可以计算每个种子节点的影响范围，因此，影响最大的所有种子节点的影响总和提供了maxσ(S)的上限，即∑u∈SAP(V,u)≥maxσ(S)∑_{u∈S}AP(V,u)≥max\\ \\sigma(S)∑u∈S​AP(V,u)≥maxσ(S)，这是利用次模函数的性质。
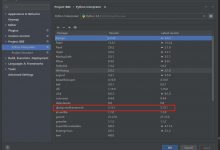
• 状态D转变为D’的概率为：
  
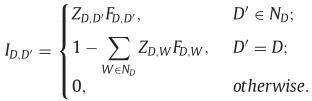
  其中ZD,D′=1K(N−K)+∣Λ(λ)∣−1Z_{D,D~\’}=\\frac{1}{K(N-K)+|\\Lambda(\\lambda)|-1}ZD,D′​=K(N−K)+∣Λ(λ)∣−11​是D的邻居集合ND产生状态D’的概率。K为种子集的大小，∣Λ(λ)∣|\\Lambda(\\lambda)|∣Λ(λ)∣为离散空间的大小。
  FD,D′F_{D,D~\’}FD,D′​为接受D’的概率：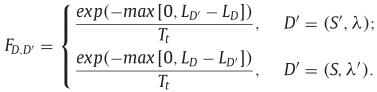
  

3.CSA提升：CSA-Q

• CSA算法由于惩罚函数涉及影响力损失[σ(S)-minσ(S-A)]的耗时计算，因此复杂函数评估会进一步加剧CSA复杂度。这促使我们使用更易处理的影响力损失计算来提高CSA的效率。
• 命题2：信息损失[σ(S)−maxσ(S−A)][\\sigma(S)-max\\sigma(S-A)][σ(S)−maxσ(S−A)]的上边界为maxΣi=1,vi∈SRσ(vi)max\\varSigma_{i=1,v_i\\in\\\\S}^{R}\\sigma(v_i)maxΣi=1,vi​∈SR​σ(vi​)，R是故障节点的数量。
• 选择考虑了影响损失后的top-K节点后，可以得到新的惩罚函数：
  LΩ′(S,λ)=−σ(S)+λ×max[0,maxΣi=1,vi∈SRσ(vi)−η]L\’_\\Omega(S,\\lambda)=-\\sigma(S)+\\lambda\\times max[0,max\\varSigma_{i=1,v_i\\in\\\\S}^{R}\\sigma(v_i)-\\eta]LΩ′​(S,λ)=−σ(S)+λ×max[0,maxΣi=1,vi​∈SR​σ(vi​)−η]
  它可以计算单个故障节点的影响范围v∈A，而不是计算（S-A）剩余节点的每个集合。与CSA相比，速度提升了很多，影响的结果是相似的。而CSA和CSA-Q均较优于其它算法。

注：

1.有待解决的问题

• 图1中第二组的选择，当v1故障时的损失？
• IMIL问题归约到IM问题。
• 可以通过预先修剪影响力损失较大的解决方案来进一步改进CSA算法。
• 实验部分略。

2.Tt参数设置的推导

命题1：温度设置Tt=q×ρln(t+1)T_t=\\frac{q\\times\\rho}{ln(t+1)}Tt​=ln(t+1)q×ρ​满足:
(a)Tt>Tt+1(a)\\ T_t>T_{t+1}(a)Tt​>Tt+1​
(b)limt→∞Tt=0(b)\\ lim_{t\\to\\infty}T_t=0(b)limt→∞​Tt​=0
(c)Tt⩾2qln(t+1)×max⁡∣LD′−LD∣(c)\\ T_t\\geqslant2\\frac{q}{ln(t+1)}\\times\\max|L_{D\’}-L_D|(c)Tt​⩾2ln(t+1)q​×max∣LD′​−LD​∣
p,q都是常量故a,b很明显，我们计算max⁡∣LD′−LD∣\\max|L_{D\’}-L_D|max∣LD′​−LD​∣对于S或λ在联合空间中发生变化的两种情况。

因此有Tt=q×ρln(t+1)=2q×max⁡σ(S)(1+maxσ(A))ln(t+1)T_t=\\frac{q\\times\\rho}{ln(t+1)}=\\frac{2q\\times\\max\\ \\sigma(S)(1+max\\ \\sigma(A))}{ln(t+1)}Tt​=ln(t+1)q×ρ​=ln(t+1)2q×maxσ(S)(1+maxσ(A))​