Python监督学习：回归

回归是最重要的统计和机器学习工具之一。我们说机器学习之旅从回归开始就没有错。它可以被定义为允许我们基于数据做出决策的参数技术，或者换句话说，允许我们通过学习输入和输出变量之间的关系来基于数据进行预测。这里，依赖于输入变量的输出变量是连续值实数。在回归中，输入和输出变量之间的关系很重要，它有助于我们理解输出变量的值如何随输入变量的变化而变化。回归经常用于预测价格，经济，变化等。

用Python构建回归量

在本节中，我们将学习如何构建单变量和多变量回归量。

线性回归器/单变量回归器

让我们重要一些必要的包 –

import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt

现在，我们需要提供输入数据，并将数据保存在名为linear.txt的文件中。

input = 'D:/ProgramData/linear.txt'

我们需要使用 np.loadtxt 函数加载这些数据。

input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]

下一步是训练模型。让我们提供培训和测试样品。

training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training

X_train, y_train = X[:training_samples], y[:training_samples]

X_test, y_test = X[training_samples:], y[training_samples:]

现在，我们需要创建一个线性回归量对象。

reg_linear = linear_model.LinearRegression()

使用训练样本训练对象。

reg_linear.fit(X_train, y_train)

我们需要用测试数据进行预测。

y_test_pred = reg_linear.predict(X_test)

现在绘制并可视化数据。

plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_test, y_test_pred, color = 'black', linewidth = 2)
plt.xticks(())
plt.yticks(())
plt.show()

输出

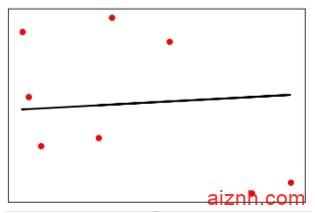
Python监督学习：回归

现在，我们可以计算线性回归的性能如下 –

print("Performance of Linear regressor:")
print("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred),
2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))

输出

线性回归器的性能 –

Mean absolute error = 1.78
Mean squared error = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09

在上面的代码中，我们使用了这个小数据。如果您想要一些大数据集，那么您可以使用sklearn.dataset导入更大的数据集。

2,4.82.9,4.72.5,53.2,5.56,57.6,43.2,0.92.9,1.92.4,
3.50.5,3.41,40.9,5.91.2,2.583.2,5.65.1,1.54.5,
1.22.3,6.32.1,2.8

多变量回归量

首先，让我们导入一些必需的包 –

import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures

现在，我们需要提供输入数据，并将数据保存在名为linear.txt的文件中。

input = 'D:/ProgramData/Mul_linear.txt'

我们将使用 np.loadtxt 函数加载此数据。

input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]

下一步是培训模型; 我们将提供培训和测试样品。

training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training

X_train, y_train = X[:training_samples], y[:training_samples]

X_test, y_test = X[training_samples:], y[training_samples:]

现在，我们需要创建一个线性回归量对象。

reg_linear_mul = linear_model.LinearRegression()

使用训练样本训练对象。

reg_linear_mul.fit(X_train, y_train)

现在，最后我们需要用测试数据进行预测。

y_test_pred = reg_linear_mul.predict(X_test)

print("Performance of Linear regressor:")
print("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))

输出

线性回归器的性能 –

Mean absolute error = 0.6
Mean squared error = 0.65
Median absolute error = 0.41
Explain variance score = 0.34
R2 score = 0.33

现在，我们将创建一个10度的多项式并训练回归量。我们将提供示例数据点。

polynomial = PolynomialFeatures(degree = 10)
X_train_transformed = polynomial.fit_transform(X_train)
datapoint = [[2.23, 1.35, 1.12]]
poly_datapoint = polynomial.fit_transform(datapoint)

poly_linear_model = linear_model.LinearRegression()
poly_linear_model.fit(X_train_transformed, y_train)
print("/nLinear regression:/n", reg_linear_mul.predict(datapoint))
print("/nPolynomial regression:/n", poly_linear_model.predict(poly_datapoint))

输出

线性回归

[2.40170462]

多项式回归

[1.8697225]

在上面的代码中，我们使用了这个小数据。如果您想要大数据集，则可以使用sklearn.dataset导入更大的数据集。

2,4.8,1.2,3.22.9,4.7,1.5,3.62.5,5,2.8,23.2,5.5,3.5,2.16,5,
2,3.27.6,4,1.2,3.23.2,0.9,2.3,1.42.9,1.9,2.3,1.22.4,3.5,
2.8,3.60.5,3.4,1.8,2.91,4,3,2.50.9,5.9,5.6,0.81.2,2.58,
3.45,1.233.2,5.6,2,3.25.1,1.5,1.2,1.34.5,1.2,4.1,2.32.3,
6.3,2.5,3.22.1,2.8,1.2,3.6

用Python构建回归量

线性回归器/单变量回归器

输出

输出

多变量回归量

输出

输出

相关推荐

热门文章

热门标签

回顶部