一. 概述
- CNN网络
- CNN网络通常用于图像的特征提取
- 组成部分
- 通常包含卷积层、池化层等
二. 边缘检测示例
- 什么是边缘检测?
- 即对图像的边缘信息进行提取
- 如下图,是对图片的垂直边缘检测和水平边缘检测
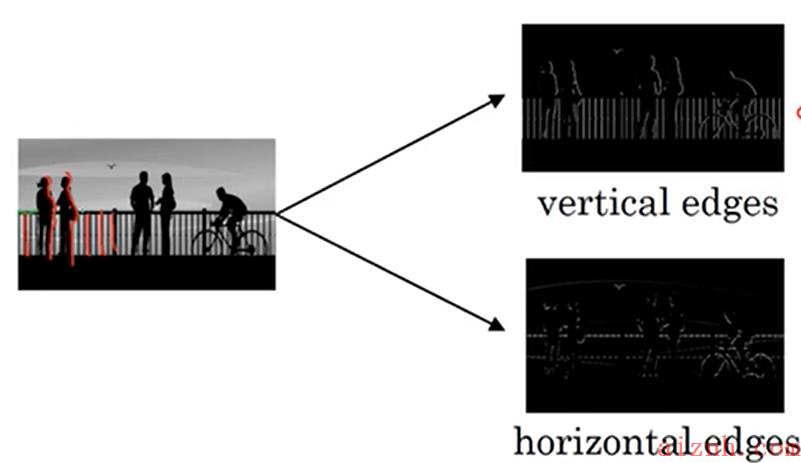
- 如何实现边缘检测?
- 就是利用CNN网络中的卷积层进行计算
- 什么是卷积计算?
- 这里以简单的二维向量举例(如下图)
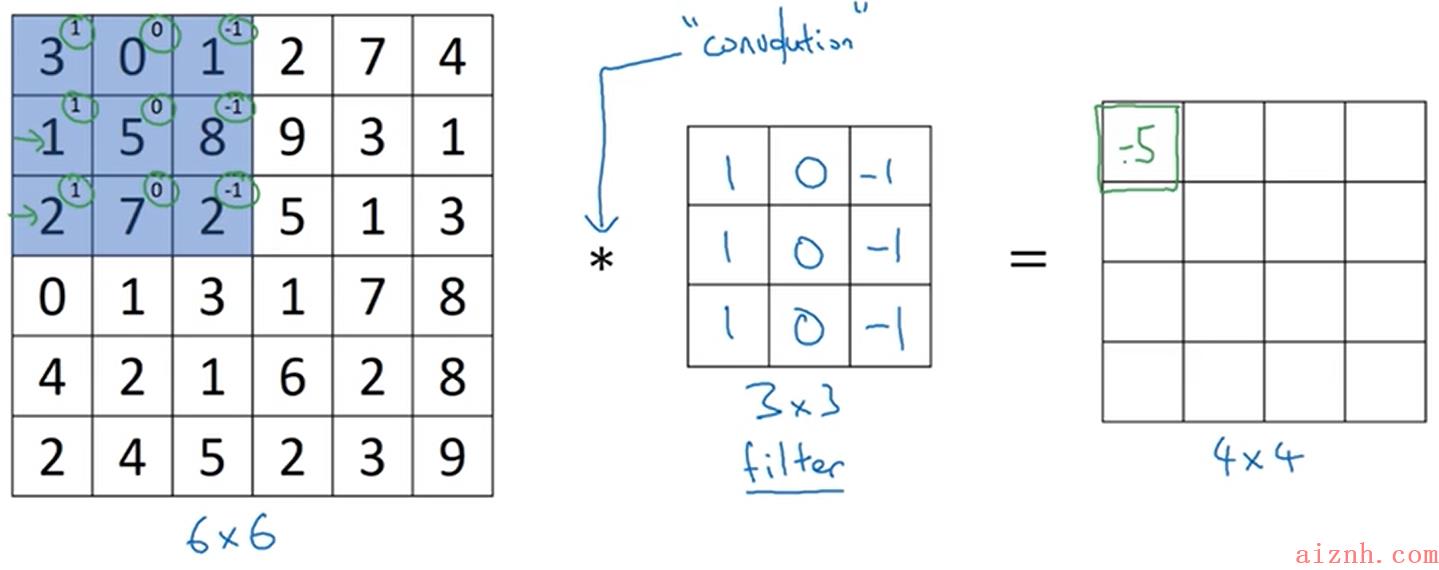
- 其中6×6代表待处理的输入,比如图片;3×3代表的是滤波器;计算结果为4×4的矩阵;其中 ∗*∗代表的是卷积操作
- 计算过程是将3×3的矩阵与图片中对应的3×3的部分的每个元素相乘再相加,如图得到第一个输出 -5 ;然后依次向右移动,再向下
- 最终的卷积计算结果如下(注意图中不同颜色方框所框住的内容)
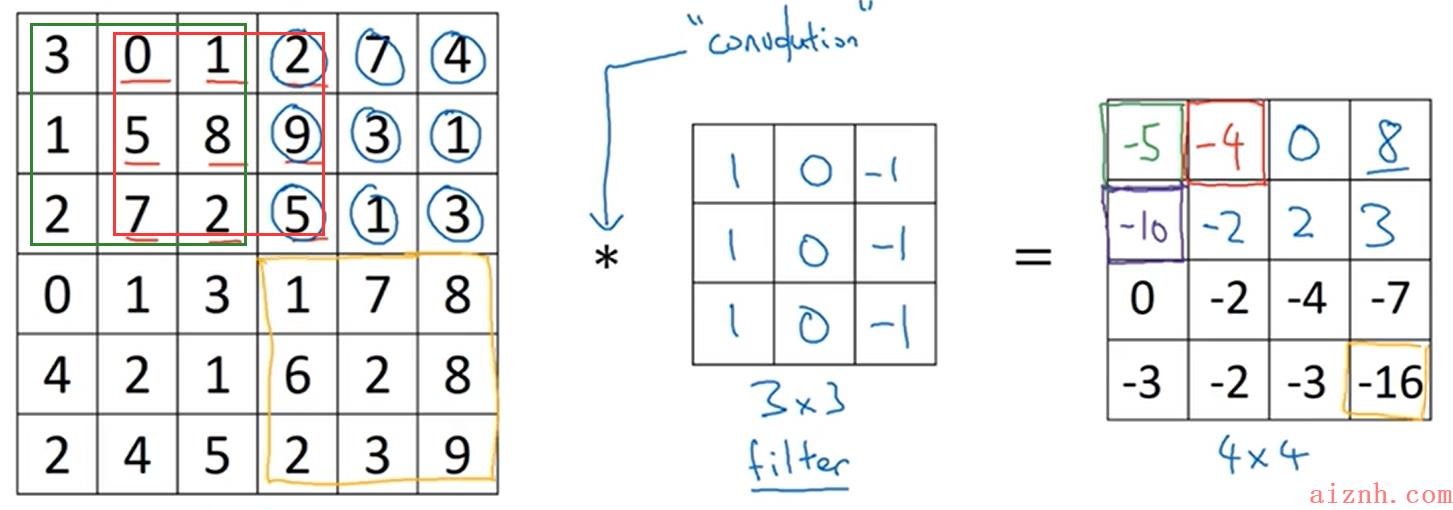
- 为什么卷积计算就可以检测边缘呢?
- 上图是对卷积计算进行一个解释,但是并不能体现出能够实现边缘检测等功能
- 所以这里举一个最简单的实例,看下图
- 假如图片的亮度和数字大小成正比,也就是数字越大,图片越亮;输入的图片黑灰之间有一条分割线需要我们去检测,那么通过卷积操作,这个垂直的地方就被放大了,更加突出

- 滤波器
- 这里想要检测什么特征主要跟滤波器有关
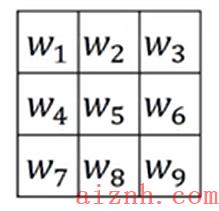
- 如下图,是检测水平和垂直边缘常用的两种滤波器

- 但是上面的滤波器只能检测固定方向的,想要检测其他角度的边缘怎么办呢
- 可以把滤波器里的参数都设置成可变的,通过对模型进行训练得到结果
- 这样得到的滤波器就十分灵活了,会根据参数的调节得到最好的结果
三. Padding(填充)
- 为什么需要Padding?
-
前面的卷积操作可以看到,输入为6×6,滤波器为3×3,得到的结果为4×4;但是这通常不是我们想得到的结果,这样每次卷积之后都变小了;我们更想输入和输出的大小相同,这样更方便计算
-
对输入和输出的维度用式子表示,输入为 n x n,卷积为 f x f,那么结果为(n-f+1)x(n-f+1)
- 如何Padding?
- 就是在输入矩阵的最外围加上一层(这个填充的层数是可以设置的,这里简单起见设置为1 )
- 假设在填充 1层,那么6×6就变成了8×8
- 抽象为式子就是(n+2* p-f+1)x(n+2* p-f+1) ,当n=6,p=1,f=3,发现结果刚好为6,就实现了输入输出维度一致
四. 卷积步长
- 什么是步长?
- 前面看到,滤波器在输入矩阵上是一次移动一格进行计算,这个也是可以设置的我们可以一次移动两格进计算,那么步长就是2
- 设步长为s,那么计算的式子如下图

五. 三维卷积
- 前面是为了方便使用二维的矩阵进行计算,但是实际计算图片时,图片的输入是三维的;例如一张1080×1080的RGB图片,会有三种原色红、绿、蓝;所以输入的是1080x1080x3的三维张量(这里的3也叫channel数)
- 三维张量如何卷积?
-
如下图,6x6x3的输入和3x3x3的滤波器进行计算得到4×4的结果,发现结果还是二维的;是因为结果中的每个元素是由27个数相加的到的(之前二维的是9个数相加)
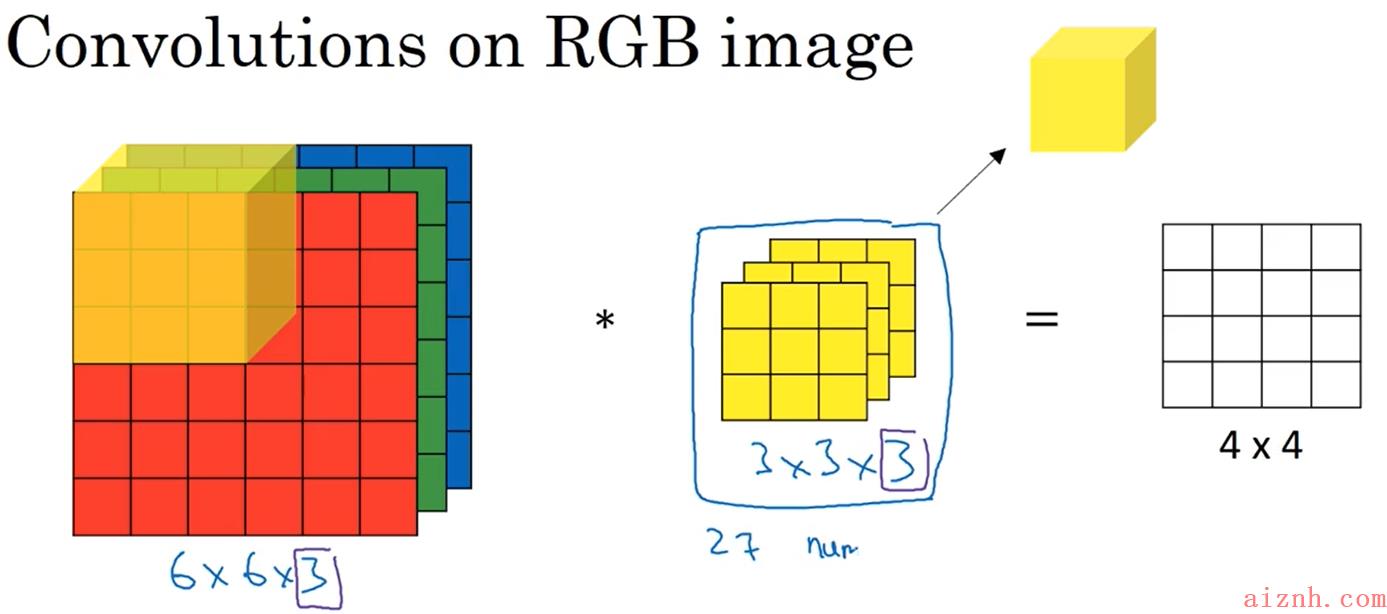
-
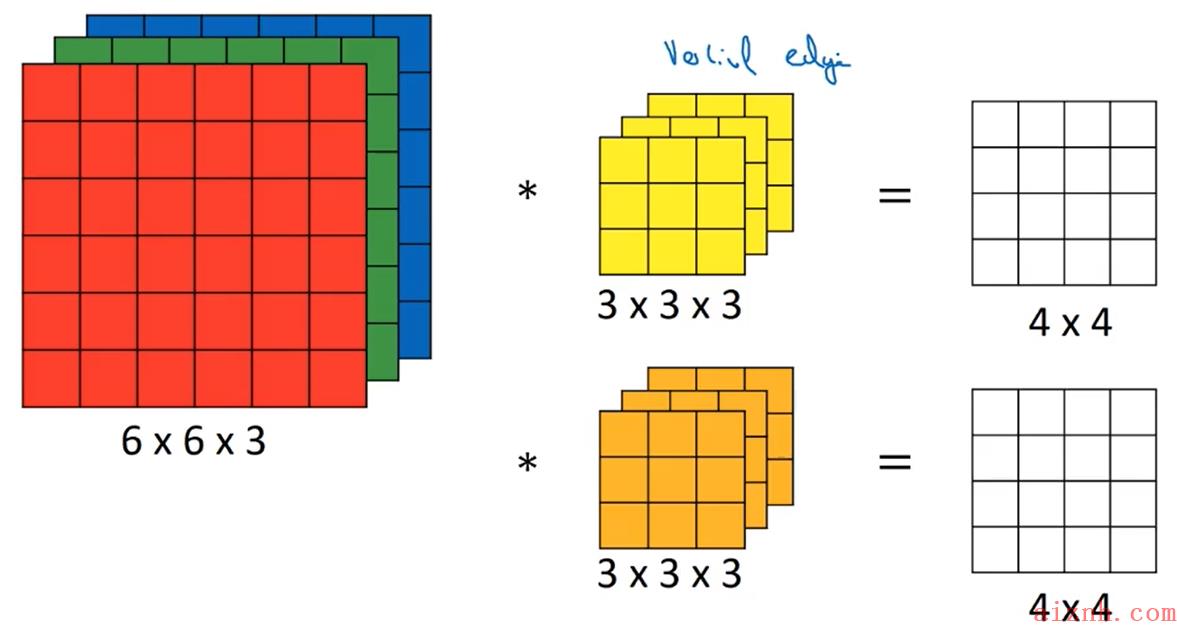
上面的输入是三维的,输出是二维的,显然不利于后续的计算(这里我们还是希望输入和输出的维度一致);所以再添加一组3x3x3的滤波器,计算得到4x4x2的结果
-
所以也可以看出来输出结果的最后一维(也就是channel),是由滤波器的组数决定的
-
所以结合一下前面的知识,对原始的输入进行Padding,然后把滤波器的组数设置为3,那么输出维度就是6x6x3了,就和输入维度一致了
-
另外,当设置每一组为不同的滤波器时(比如第一组为水平检测滤波器,第二组为垂直检测滤波器),那么就实现了不同的边缘检测,换句话说,就是提取了不同的特征
六. Pooling(池化)
- 什么是池化?
- 池化是为了减少计算量而设计的
- 如何进行池化?
- 以最大池化为例,就是取2×2格子的最大值,依次取最大值即可,十分简单,也没有参数

- 常见的池化层
- Max Pooling:取最大值
- Average Pooling:取平均值
 爱站程序员基地
爱站程序员基地









