08:vigenère密码
1)Vigenére密码 (1) Vigenére Cipher)
This technique is an example of Polyalphabetic Substitution technique which uses 26 Caesar ciphers make up the mono-alphabetic substitution rules which follow a count shifting mechanism from 0 to 25. That is, for each plain-text character we have a corresponding substitution known as a key letter.
该技术是使用26个凯撒密码弥补随后的计数移动机构从0到25。也就是说,对于我们的相应取代已知为每个纯文本字符的单字母替换规则多码替代技术的一个例子关键信 。
To understand this technique we need to take a look on this Vigenére tableau.
要了解此技术,我们需要看一下Vigenére表格 。

The logic for this technique is simple, say for a key letter \’t\’ and plain-text letter \’h\’, the corresponding cipher-text letter is at the intersection of row titled \’t\’ and column titled \’h\’ thus for this case we get a ciphertext that would be \’A\’ based on above table.
这种技术的逻辑很简单,例如对于一个关键字母“ t”和纯文本字母“ h” ,相应的密文字母位于标题为“ t”的行与标题为“ h”的列的交点处。情况下,根据上表,我们将得到一个密文“ A” 。
It is clear that for encrypting a plain-text message we must need a key whose length is equal to the size of the plain-text message usually a repeating key is used.
显然,为了加密纯文本消息,我们需要一个长度等于纯文本消息大小的密钥,通常使用重复密钥。
2)Playfair密码 (2) Playfair Cipher)
Playfair cipher (aka Playfair square) is a cryptography technique used for manual encryption, it was introduced by Charles Wheatstone in 1854 but it was popularized by Lord Playfair hence his name used.
Playfair密码(又名Playfair平方)是一种用于手动加密的加密技术,由Charles Wheatstone于1854年提出,但后来被Playfair勋爵推广,因此使用了他的名字。
The Playfair cipher was used in world war I by the British army and in World war II it was used by Australians. It was because the Playfair cipher is quite fast to use and does not demand any special equipment.
Playfair密码在第一次世界大战中被英国军队使用,在第二次世界大战中被澳大利亚人使用。 这是因为Playfair密码使用起来非常快,并且不需要任何特殊设备。
Playfair technique has 2 major steps:
Playfair技术有两个主要步骤:
 .minHeight{min-height: 250px;}@media (min-width: 1025px){.minHeight{min-height: 90px;}}.minHeight{min-height: 250px;}@media (min-width: 1025px){.minHeight{min-height: 90px;}}
.minHeight{min-height: 250px;}@media (min-width: 1025px){.minHeight{min-height: 90px;}}.minHeight{min-height: 250px;}@media (min-width: 1025px){.minHeight{min-height: 90px;}}
Step 1: Creation and Population of matrix
步骤1:矩阵的创建和填充
This technique uses a 5 x 5 matrix which stores a keyword (or phrase) that becomes the key for encryption or decryption. This involves some set of fixed rule, those are:
该技术使用5 x 5矩阵 ,该矩阵存储一个关键字(或短语),该关键字成为加密或解密的密钥。 这涉及到一些固定规则,它们是:
-
Fill the keyword in the matrix row-wise from left to right, top to down.
从左到右,从上到下按行在矩阵中填充关键字。
-
Remove all repeated letters.
删除所有重复的字母。
-
Enter the remaining spaces in the matrix with the rest of the English alphabets (A-Z) that were not a part of our keyword. In this process, combine I and J in the same cell of the table; in other words, if I and J is a part of the keyword disregard both I and J while filling the remaining slots.
在矩阵中输入剩余的空格以及不属于我们关键字的其余英文字母( AZ )。 在此过程中,将I和J合并到表的同一单元格中; 换句话说,如果I和J是关键字的一部分,则在填充其余插槽时,请同时忽略I和J。
Example:
例:
Let\’s take our keyword as \’INCLUDEHELP IS AWESOME\’. Then 5 x 5 matrix will look as:
让我们将关键字设为“ INCLUDEHELP IS AWESOME” 。 然后5 x 5矩阵将如下所示:

Step 2: Encryption
步骤2:加密
This process consist of the following process:
此过程包括以下过程:
-
The plain-text we want to encrypt need to broke down into a pair of alphabets. For example, if our message is \”MY NAME IS POGO\”, it will become \”MY NA ME IS PO GO\”.
我们要加密的纯文本需要分解为一对字母。 例如,如果我们的消息是“ MY NAME IS POGO” ,它将变成“ MY NA ME IS PO GO” 。
-
If both alphabets are the same (or only left), add an X after the first alphabet in a pair. Encrypt the new pair (after adding X) then continue.
如果两个字母相同(或仅向左),则在成对的第一个字母之后添加X。 加密新对(添加X之后 ),然后继续。
If pair appears in the same row of the matrix, replace them with a letter at its right, if it\’s at the right end of the row then wrapping around the left side of the row.
If pair appears in the same column of the matrix, replace them with the alphabet below them. If it\’s on the bottom then wrapping around the top of the row.
如果对出现在矩阵的同一列中,请用其下面的字母替换它们。 如果它在底部,则环绕该行的顶部。
If the pairis not in the same row or column, replace them with the alphabets in the same row respectively, but at the other pair of cornersof the rectangle defined by the original pair. The order is quite significant here. The first encrypt alphabet of the pair is the one that is present on the same row as the first plaintext alphabet.
如果该对不在同一行或同一列中,则分别用同一行中的字母代替它们,而应替换为原始对定义的矩形的另一对角。 这里的顺序非常重要。 该对中的第一个加密字母是与第一个明文字母在同一行上的字母。
Explanation:
说明:
\”MY NA ME IS PO GO\”
“我不喜欢我”
So we start with MY now in the above matrix it was not in the same row or column then rule 5 will apply.
因此,我们从上面的矩阵中的MY开始,因为它不在同一行或同一列中,所以将应用规则5。

Now we replace \’MY\’ with the diagonals that are \’KZ\’.
现在我们将对角线KZ替换为MY 。
Let\’s move to \’NA\’ again they are not in the same row or column, rule 5 will apply.
让我们再次移至“ NA”(它们不在同一行或同一列中),将应用规则5。

Now, \’NA\’ will be replaced with \’UE\’.
现在, “ NA”将被替换为“ UE” 。
Similarly, \”MY NA ME IS PO GO\” will become \”KZ UE FA LO DS BS\”.
类似地, “ MY NA ME IS PO GO”将变为“ KZ UE FA LO DS BS” 。
For the decryptionprocess, we will just follow the exact opposite steps.
对于解密过程,我们将遵循完全相反的步骤。
.minHeight{min-height: 250px;}@media (min-width: 1025px){.minHeight{min-height: 90px;}}.minHeight{min-height: 250px;}@media (min-width: 1025px){.minHeight{min-height: 90px;}}
3)希尔密码 (3) Hill Cipher)
The Hill cipher is based on polygraphic substitution that is it works on multiple letters at the same time, introduced by Lester Hill in 1929. This method related to the matrix theory of mathematics, specifically how to compute the inverse of a matrix.
希尔密码是基于多重图形替换的,它同时处理多个字母,这是莱斯特·希尔(Lester Hill)在1929年提出的。这种方法与数学的矩阵理论有关,特别是如何计算矩阵的逆。
Let\’s see how it works:
让我们看看它是如何工作的:
-
Every Letter of plain-text will be represented by a number, so that A=0, B=1,…,Z=25.
每个纯文本字母将由一个数字表示,因此A = 0,B = 1,…,Z = 25 。
-
We will make a matrix of the plain-text message using the above knowledge.
我们将使用以上知识来构成纯文本消息的矩阵。
For example,
例如,
\’CAT\’, so C=2, A=0, T=19. Thus our matrix lookslike:
\’CAT\’ ,因此C = 2,A = 0,T = 19 。 因此我们的矩阵看起来像:
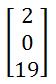
-
Now, we multiply our matrix with randomly chosen keys. The size of the key must be n x n where n is a number of rows of our plain-text matrix.
现在,我们将矩阵与随机选择的键相乘。 键的大小必须为nxn ,其中n是纯文本矩阵的行数。
For example:
例如:
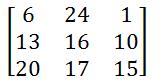
-
Now multiply the above matrices,
现在将上述矩阵相乘,
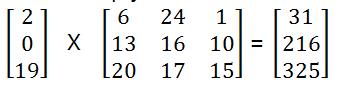
-
Now we will calculate a mod 26 value of the above matrix, that is remainder after dividing 26.
现在我们将计算上述矩阵的mod 26值,即除以26后的余数。
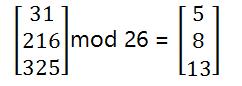
-
Translate back number to alphabets, 5=F, 8=I, 13=N. Therefore, our cipher-text is \”FIN\”.
将数字转换回字母,即5 = F , 8 = I , 13 = N。 因此,我们的密文为“ FIN” 。
-
For Decryption, take the cipher-text matrix and multiply it with the inverse of our original key matrix:
对于解密,请采用密文矩阵并将其与原始密钥矩阵的逆矩阵相乘:
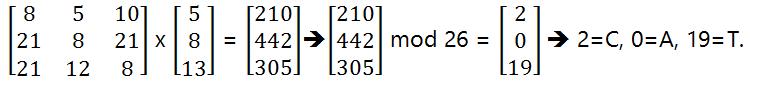
翻译自: https://www.includehelp.com/cryptography/cryptographic-techniques-vigenére-cipher-playfair-cipher-hill-cipher.aspx
08:vigenère密码
 爱站程序员基地
爱站程序员基地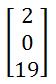
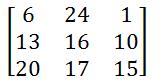
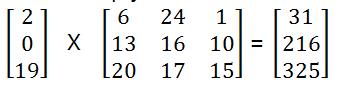
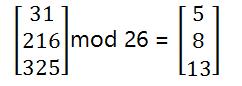
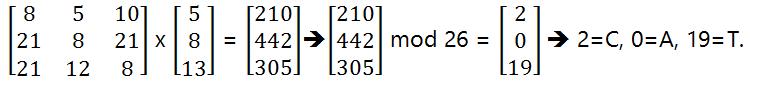
![[翻译] Backpressure explained — the resisted flow of data through software-爱站程序员基地](https://aiznh.com/wp-content/uploads/2021/05/10-220x150.jpeg)