机器学习入门实战——基于knn的airbnb房租预测

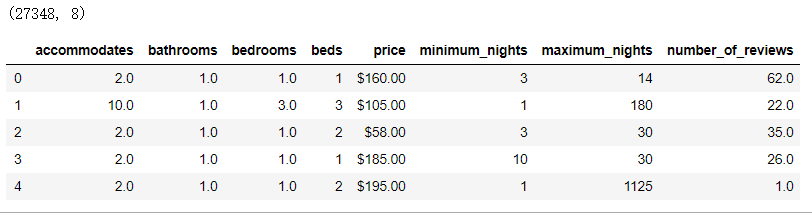
数据读取

import pandas as pdfeatures=[\'accommodates\',\'bathrooms\',\'bedrooms\',\'beds\',\'price\',\'minimum_nights\',\'maximum_nights\',\'number_of_reviews\']dc_listings=pd.read_csv(\'listings.csv\')dc_listings=dc_listings[features]print(dc_listings.shape)dc_listings.head()

运行结果：

K:候选对象个数，近邻数（如找3个和自己最近的样本）

先使用可容纳旅客的数量（accommodates）做一个简单计算，统计与可容纳3个旅客相减的情况（当前要估计价格的可容纳旅客数为3个）

import numpy as npour_acc_value=3#房间数为3个dc_listings[\'distance\']=np.abs(dc_listings.accommodates-our_acc_value)#为dc_listings新增distance列，用于保存当前房间数与3的差值dc_listings.distance.value_counts().sort_index()#统计各差值的情况

输出：

0.0      33701.0     179671.5         22.0      38653.0      12504.0       2215.0       3346.0        587.0       1258.0        159.0        4410.0        511.0       1412.0        513.0       73Name: distance, dtype: int64
原始数据统计过程中可能会存在一些规律，一般需要进行洗牌操作，打乱原有秩序（使用sample函数）

dc_listings=dc_listings.sample(frac=1,random_state=0)#洗牌 frac：抽取行的比例，1为100%  random_state:0表示不得取重复数据 1表示可以取重复数据dc_listings=dc_listings.sort_values(\'distance\')#统计差值（房间数-3）的情况 将dc_listings按照distance列排序 将和房间数3最近的放在最前面dc_listings.price.head()#取前5条的价格 由于数据时乱的，所以id和price均无规律

输出结果：

2732     $129.0014798    $249.0027309    $170.0020977    $169.0011178    $100.00Name: price, dtype: object

对价格进行类型转换，去掉$符号，转换成float,然后对前五个价格取均值，用前5个的均值来预测当前房价

dc_listings[\'price\']=dc_listings.price.str.replace(\"\\$|,\",\'\').astype(float)mean_price=dc_listings.price.iloc[:5].mean()mean_price

输出：163.4

拿75%的数据作为训练集，25%的数据作为测试集来进行模型的评估，训练集和测试集不可重复。

dc_listings.drop(\'distance\',axis=1)#删除distance列train_df=dc_listings.copy().iloc[:20544]#27392*0.75行为训练集test_df=dc_listings.copy().iloc[20544:]#剩下的作为测试集（27392*0.25）

基于单变量预测价格

#new_listing_value:当前样本的feature_clolumn（如accomodates）列属性取值#feture_column:计算房租使用的单属性def predict_price(new_listing_value,feature_column):temp_df=train_df#使用训练集来预测测试集房租结果dc_listings[feature_column]=train_df[feature_column].astype(float)#统一将格式转换成float否则会报错temp_df[\'distance\']=np.abs(train_df[feature_column]-new_listing_value)temp_df=temp_df.sort_values(\'distance\')knn_5=temp_df.price.iloc[:5]predict_price=knn_5.mean()return(predict_price)

对测试集的每一条记录使用accomodates属性预测其房租价格

#new_listing_value的值即为accommodates的取值test_df[\'predicted_price\']=test_df.accommodates.apply(predict_price,feature_column=\'accommodates\')test_df.predicted_price.head()

输出：

14122    134.023556    418.016317    134.026230    134.019769    134.0Name: predicted_price, dtype: float64

root mean square error(RMSE)均方根误差

得到每个样本的预测值后计算均方根误差用于评估模型（值越小模型越好）

test_df[\'squared_error\']=(test_df[\'predicted_price\']-test_df[\'price\'])**(2)mse=test_df[\'squared_error\'].mean()rmse=mse**(1/2)rmse

输出结果：

348.689169172284

试试不同的变量（属性）

for feature in [\'accommodates\',\'bedrooms\',\'bathrooms\',\'number_of_reviews\']:test_df[\'predicted_price\']=test_df[feature].apply(predict_price,feature_column=feature)test_df[\'squared_error\']=(test_df[\'predicted_price\']-test_df[\'price\'])**(2)mse=test_df[\'squared_error\'].mean()rmse=mse**(1/2)print(\"RMSE for the {} column:{}\".format(feature,rmse))

输出：

RMSE for the accommodates column:348.689169172284RMSE for the bedrooms column:344.64855009943RMSE for the bathrooms column:361.1230782594195RMSE for the number_of_reviews column:383.4946020709275

注:由于每个测试集中的样本都要与训练集中样本一一比对，所以上述程序运行时间较长，需要耐心等待……

标准化

同时使用多个属性——如房间数（个位数）和房间面积（几十甚至上百）进行计算的时候，由于变量取值范围的不同（取值范围大的影响较大）会导致对计算结果的不良影响（如计算欧式距离时，房间面积差值平方计算结果通常较大，而房间数差值平方较小），而各个属性是独立的即它们是同等重要的，所以需要对数据进行标准化，如采用z-score标准化或归一化等手段进行预处理

z-score 标准化（Z-score normalization）

要求数据总体均值μ=0 标准差σ=1

转换公式如下：

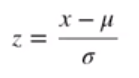
其中μ为原始数据均值,?σ为原始数据标准差,经过处理后的数据均值为0，标准差为1。 x-μ是为了让数据以0为中心分布，除以标准差σ是让所有列的取值范围相近（某一列取值范围小，标准差也相对较小，除以标准差后值会变大，反之，某一列取值范围大，标准差也较大，除以标准差后结果就会变小，这样就达到了使所有列取值范围相近的目的）。(分子和分母都是计算和均值的差值，分子是个体差值，分母是平均差值——标准差)比如让房间面积和房屋个数的取值范围相同。

标准差（又叫均方差，标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。）计算公式

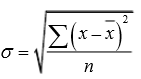
归一化（Min-Max scaling或normalization,也称为0-1归一化）

转换公式如下：

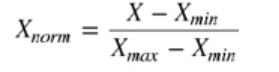
归一化将数字取值范围转换为0-1之间

经过上述处理后，只会改变原始数据的取值范围，而不会改变其分布规则（所有的数据处理都必须遵循的原则）。标准化会减小数据的取值范围，并使数据以0为中心分布。归一化使数据都分布在0-1之间。下面使用sklearn的preprocessing库进行预处理

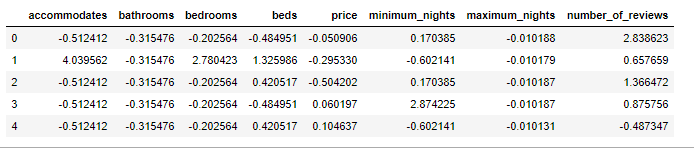
import pandas as pdfrom sklearn.preprocessing import StandardScaler#从sklearn导入标准化处理库features=[\'accommodates\',\'bathrooms\',\'bedrooms\',\'beds\',\'price\',\'minimum_nights\',\'maximum_nights\',\'number_of_reviews\']dc_listings=pd.read_csv(\'listings.csv\')dc_listings=dc_listings[features]dc_listings[\'price\']=dc_listings.price.str.replace(\"\\$|,\",\'\').astype(float)dc_listings=dc_listings.dropna()#去除空数据dc_listings[features]=StandardScaler().fit_transform(dc_listings[features])#数据标准化normalized_listings=dc_listingsprint(dc_listings.shape)normalized_listings.head()

输出结果：

(26728, 8)

#获得标准化后的测试集和训练集norm_train_df=normalized_listings.copy().iloc[0:20544]norm_test_df=normalized_listings.copy().iloc[20544:]

使用scipy（一种专门用于统计学的工具库）中的工具计算欧式距离

from scipy.spatial import distancefirst_listing=normalized_listings.iloc[0][[\'accommodates\',\'bathrooms\']]sixth_listing=normalized_listings.iloc[5][[\'accommodates\',\'bathrooms\']]first_sixth_distance=distance.euclidean(first_listing,sixth_listing)#计算第一个样本点和第六个样本点之间的欧式距离first_sixth_distance

输出：

2.275986934945609

多变量KNN模型

def predict_price_multivariate(new_listing_value,feature_columns):temp_df=norm_train_dftemp_df[\'distance\']=distance.cdist(temp_df[feature_columns],[new_listing_value[feature_columns]])#cdist用于计算训练集到测试集的向量的距离，函数每次接收一个测试集向量temp_df=temp_df.sort_values(\'distance\')knn_5=temp_df.price.iloc[:5]predicted_price=knn_5.mean()return(predicted_price)cols=[\'accommodates\',\'bedrooms\']#axis=1表示按行计算，针对测试集的每个向量均调用函数一次norm_test_df[\'predicted_price\']=norm_test_df[cols].apply(predict_price_multivariate,feature_columns=cols,axis=1)norm_test_df[\'squared_error\']=(norm_test_df[\'predicted_price\']-norm_test_df[\'price\'])**[2]mse=norm_test_df[\'squared_error\'].mean()rmse=mse**(1/2)print(rmse)

输出：

1.2069982434803874

使用SKlearn来实现KNN¶

from sklearn.neighbors import KNeighborsRegressorcols=[\'accommodates\',\'bedrooms\']knn=KNeighborsRegressor(n_neighbors=100)#实例化，参数默认值是5（默认使用5个最近邻）该参数并不是越大越好（取500比取100的时候rmse反而增加了）knn.fit(norm_train_df[cols],norm_train_df[\'price\'])#使用训练集建立模型，确定X和Ytwo_features_predictions=knn.predict(norm_test_df[cols])#对测试集的Y（价格）进行预测

使用SKlearn计算RMSE

from sklearn.metrics import mean_squared_errortwo_features_mse=mean_squared_error(norm_test_df[\'price\'],two_features_predictions)two_features_rmse=two_features_mse**(1/2)print(two_features_rmse)

输出：

0.9981501570648538

注：使用SKlearn实现KNN，感觉到速度比自己写的要快许多
加入更多的特征

cols=[\'accommodates\',\'bedrooms\',\'bathrooms\',\'beds\',\'minimum_nights\',\'maximum_nights\',\'number_of_reviews\']knn=KNeighborsRegressor(n_neighbors=100)knn.fit(norm_train_df[cols],norm_train_df[\'price\'])seven_features_predictions=knn.predict(norm_test_df[cols])seven_features_mse=mean_squared_error(norm_test_df[\'price\'],seven_features_predictions)seven_features_rmse=seven_features_mse**(1/2)print(seven_features_rmse

输出：

0.9704297561523479

可以看到，当特征值增加到7个的时候，误差（rmse）变小了

总结

由于KNN的计算方式，其一般只可用于数据规模较小的情况下。另外，KNN也可以用于分类任务，只不过这时候样本的label是类别而不是数值。同样，也可以跟每个样本进行对比，取前n个最近邻，看大多数属于哪个类别，则认为当前样本属于哪个类别。