大量最新的研究正致力于将深度学习网络用于实现一些基本的机器人操作,那么反过来看,机器人领域的一些研究成果是否有可能应用于指导软件开发?在上周三(9 月 26 日)发布的一项最新研究中,谷歌大脑的研究人员 Aleksandra Faust,以及她在圣地亚国家实验室和新墨西哥大学的合作研究者们,引入机器人领域的研究对软件程序开发做了全新阐释。在该项研究中,软件程序被视为一种在不确定的领域中探索轨迹的机器人,由此引入强化学习方法实现可更好处理不确定性的韧性软件。论文进一步将该理论实际应用于排序算法,实现了一种称为 RL 排序的韧性算法。实验表明,相比于经典排序算法,RL 排序算法对需排序数组的操作次数更少,同时在引入错误的情况下能给出更接近于正确的结果。
该论文以“Resilient Computing with Reinforcement Learning on a Dynamical System: Case Study in Sorting”为名最新发布在 ArXiv 上,它已被第 57 届 IEEE 决策和控制会议(ICDC,IEEE Conference on Decision and Control)收录。论文主要贡献人 Faust 博士的研究领域主要是机器人和无人驾驶汽车。在一些先期工作中,她使用强化学习训练机器人,实现在地面和空中未知路线中的行走。
该论文主要针对软件开发领域问题。软件程序在开发中,通常并未考虑“韧性”(resiliency)和“稳定性”(stability),即程序是否可以从诸如内存芯片崩溃等一些开发中并未虑及的问题下存活。虽然软件开发的最佳实践一直在与时俱进,正如设计模式和正确性证明等,但是现有研究并未考虑到编程人员会出错误的问题,也没有考虑当失败条件或是错误出现时,程序运行过程中会表现出怎样的行为。由此,Faust 等人提出了引入机器人研究领域的方法去改进软件开发方法,采用“基于目标的任务”面对错误问题。为测试论文所提出的理论,论文研究者以数组排序为实际用例,实现了一种新的智能体。排序任务是计算机科学中的一个经典问题,可作为测试新软件方法的一个好任务。该程序称为 RL 排序算法,它使用强化学习的方法最大化回报,使用马尔科夫决策过程从变量空间的可能移动中做出选择。由此,排序程序的计算过程变成“在变量空间中的轨迹问题”。时间每推进一次,程序搜索“状态”和程序变量会发生相应的改变,进而发现用于正确排序数组元素的行动轨迹。论文进而对比测试了两种经典排序算法,即快排和冒泡排序。实验表明,在引入 5% 错误条件的情况下,虽然两种经典算法很快会出错,但论文提出的强化学习(RL)排序算法依然可以正确的执行。另一方面,在出现错误时,RL 排序算法给出的结果要更接近于完全正确排序的数组。此外,RL 排序算法在实现排序中操作的数组元素更少,因此性能也要优于其它两种对比方法。
下面,我们将详细介绍该论文的理念和方法。
问题的提出
现代软件已经控制了交通系统、股票市场、制造工厂等承担高度责任的系统。软件运行于各种大相径庭的操作环境中,这些环境往往超出软件先前的设计范围。一些软错误、随机或临时错误会对计算的各个方面产生影响,例如内存、注册表和计算等。如果这些错误并未被检测到或是没有有效管理,那么它们的累加效应将会十分严重。例如,太空环境、高海拔地区和反应堆周边的粒子和电磁辐射会日积月累地导致一些软件错误。同样,当前微芯片设计正在挑战着物理极限,其中会导致出现一些内存错误和软件计算错误。传统的辐射加固和容错计算是采用物理冗余系统和物理防护层实现的,但是此类做法会增加系统的复杂性和实现代价。由此,可适应错误并在错误条件下保持工作的韧性算法(Resilient algorithms)备受人们关注。
现代应用需要算法可在有限的资源下工作。例如,算法不允许自行终止,而是会根据更高的优先级产生中断,并且生成的部分结果必须要比输入数据的质量更好。一个韧性算法的基本需求,包括提前终止(Early Termination)和稳定地推进到解决结果。
但是,传统计算的工作通常基于两个基本假设,即正确性和由程序发起终止。理论计算科学认为,一个算法在给定正确输入的情况下,只有终止并返回正确的计算结果才可以称为是“完全正确”(totally correct)。通过提供代码检查、设计模式和正确性验证等最佳实践,完全正确影响了传统软件工程,防止出现错误的规范和由开发人员引入的软件缺陷。完全正确并未对计算随时间演变的情况做任何限制。只要计算的输入是正确的,那么结果就应该是正确的。这种方式会带来两种后果。首先,整体正确性对于存在于输入或程序依赖上的错误不具备韧性。其次,如果算法提前终止,那么算法的输出情况没有任何保证。
本论文提出将控制领域中的“韧性”和“稳定性”应用于计算领域,目的是解决存在于完全正确性和提取终止问题上的限制。论文借鉴了机器人操作和软件开发上的相似性,将计算看成是一种在程序变量空间中的轨迹生成问题。基于此,论文指出将计算程序定义为一种由程序变量所定义的向量空间上的离散时间动态系统,受控于具有正确输出平衡的向量转换矩阵。通过提出马尔科夫决策过程(MDP)的回报函数,可使用强化学习控制李雅普诺夫函数的求解。论文将李雅普诺夫(Lyapunov)稳定性理论用于分析所生成受控系统的等价性,为向目标稳定推进给出了理论上的保证,并给出了存在软错误情况下取得成功的概率。为了展示控制和决策制定工具对算法设计的影响,论文具体实现了一个计算机科学中的经典问题,即数组排序。
论文的主要创新是,提出了一种将顺序的、基于状态的计算过程描述为马尔科夫决策过程的方法,以及一种对强化学习和李雅普诺夫稳定性理论的新颖应用,实现了在具有很高软错误概率(大于 50%)的环境中的韧性排序算法。具体而言,主要贡献包括:一、提出了一种实现韧性计算的受控动态系统构建方法;二、实现了一种用于排序算法的强化学习智能体;三、通过进一步的实验分析了算法的稳定性和韧性。
背景知识
时移轨迹生成(Trajectory generation over time)可以看成是一个时间离散的、受控的、非线性的动态系统在时刻 n 的状态,即:
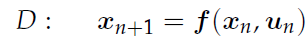
其中,D 称为状态转移函数,f 是一种非线性函数,x∈X 为系统状态,u∈U 为影响系统的输入(即动作)。u 的状态会随时间发生变化。
在一个确定性 MDP 中,元组(X,U,D,R)指定了一个标量回报函数,R:X→R。MDP 的解给出了一种控制策略 π: X→U,实现智能体生命周期中的折算累积回报(discounted cumulative reward)的最大化,即状态价值函数 (state-value function) :
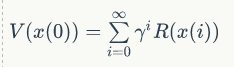
其中γ∈[0,1]。
强化学习通过与系统交互对 MDP 进行求解。RL 适用于状态转移函数 D 或回报函数 R 未知的情况。RL 使用近似值迭代(AVI,Approximate Value Iteration)逼近特征图(feature map),发现近似最优状态价值函数 V:X→R:
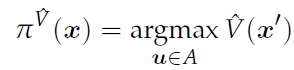
AVI 分为两个阶段,即学习阶段和轨迹生成阶段。在学习阶段,输入是用户提供的特征向量 F(x),根据期望最大(EM)学习权重θ。在完成学习阶段后,AVI 进入轨迹生成阶段。它输入一个初始状态、特征向量和学习的参数,使用贪心闭循环控制策略生成轨迹,考虑状态价值近似为:
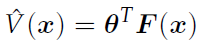
其中,x
是在状态 x 上应用动作 u 的结果,即 x
=D(x,u)。AVI 适用于很多问题。
李雅普诺夫稳定性理论提供了一种评估平衡(Equilibrium)稳定性的工具。如果两个初始条件随时间互相收敛,那么称达到了平衡,即李雅普诺夫全局渐进稳定的。李雅普诺夫直接法为初始状态的稳定性提供了充分条件。该方法需要为状态构建一个正定标量函数 W:X→R,该函数沿轨迹单调递减,并在达到平衡状态时递减为 0。该函数可宽松理解为系统的能量,因此函数值是正值,并且随时间递减,直到消耗殆尽并停止。实践中,可以使用李雅普诺夫稳定性理论评估强化学习规划动作任务的完成。具体方法包括选择一个预确定控制方式以保证任务完成,或者构建一个状态价值函数去控制李雅普诺夫函数。本论文使用了后一种方法。
问题定义与一般方法
一个确定性程序的输出取决于两个因素,即程序变量的初始状态,以及解决问题的步骤和算法过程。如果将程序开发看成是一个动态系统,那么控制流构件(if-then-else、循环等)是控制器开关,指令是在离散时间方式下按内部时钟节奏执行的,状态转移由指令注册表中的待执行指令确定。这样,程序就是一种用于动态系统的控制策略,它由变量状态随时间的改变情况确定,直至计算结束。计算则是程序变量空间中的一个轨迹,从变量的某个初始状态开始(即初始向量),结束于目标状态(即目标向量)。
在程序运行时,内部变量和指令计数器的位置唯一确定了程序的状态,即配置(configuration)。计算解决的是一个物理程序进入某个配置的方式问题。由此,程序的状态空间由所有变量值的空间构成,该空间满足马尔科夫性质。如果假设所有的变量均为实数,那么具有 d 个变量的程序的状态是 X=R(d) 构成了一个 d 维向量。赋值、算术运算和更改指令等操作和编程控件改变了向量,共同构成了动作空间(action space)。可以证明,如此构建的配置是一个非线性动态系统,其中状态为向量,操作是向量变换,可表示为矩阵转换。也就是说,一个具有 d 个本地变量和赋值、求和和交换操作的程序 P,是一种非线性离散事件和输入系统,可形式化地表述为:
其中状态 xn 是 d 维实数空间,M 是状态空间的向量转换矩阵。由此,操作所有变量的程序就构成了一个非线性控制系统,可将控制理论应用于程序分析。
在将程序形式化为动态系统 (X,U, D) 后,我们只需要定义一个回报函数,就可构成形式化的 MDP。回报是状态向量上的标量反馈。通常只有在达到目标时,或是使用状态的度量可用时,才会给出回报。
使用强化学习的排序智能体
论文以排序的实现为例,给出回报的具体形式化定义,进而提出一种稳定和韧性的强化学习排序智能体。该实现方法只需在小规模数组上做一次学习,就可以使用学习到的策略对任意长度的数组排序。实现方法的基本步骤如下:
第一步:定义 MDP。数组排序状态空间是一个 d 个元素的数组 X,控制空间是可能元素重定位的离散集合 U。Action(i,j) 是一组插入操作,将数组的第 i 个元素移除,插入到第 j 个位置。将该数组看成是向量,那么动作就是对向量坐标的排列,可表示为矩阵的转换。
第二步:定义回报函数。回报函数包括两部分:近邻元素移动的总和,加上实现排序数组的回报。
第三步:定义状态价值函数,近似最优状态价值函数 V。在此选择的特性优先考虑未排序程度最大的数组区域,因为目标是让智能体在有限资源的情况下达到执行次数的最大化。
最后,一旦使用强化学习完成特征权重的学习,强化学习排序智能体进入轨迹生成阶段,这时无需使用进一步的学习对数组排序。在每个时间步,算法会评估当前的数组,选择需要移动到新位置的元素。轨迹生成中会并选定使收益最大化的动作,并将其应用于数组。一但数组中没有需要调整位置的元素,算法停止,数组完成排序。
论文从理论上分析了算法满足稳定性和韧性。虽然算法的时间复杂度可达 O(d*d),但是在可并行计算情况下,时间复杂度可降至 O(logd),空间复杂度为 O(d)。算法的具体理论和证明过程,可参见原论文。
实验结果
强化学习(RL)排序算法在学习智能体参数时,采用了对离散动作运行 AVI。训练智能体时根据经验使用了 15 轮迭代,生成参数包括了所有的负向元素。作为对比算法,冒泡排序算法反复扫描数组,并交换近邻的无序元素。而快排算法则会选定一个锚点元素,基于此创建大于、小于和等于锚点的三个子列表,在大于和小于子列表上做递归排序,最终将三个列表归并在一起。快排是一轮扫描算法,其中数组元素位置变动较大。而冒泡排序中,数组元素每次位置更改较小,但位置更改更为频繁。实验所用数据集包括 100 个具有 10 到 100 个随机抽取元素的数组,并在无错误和存在 5% 错误两种情况下衡量了算法的性能。
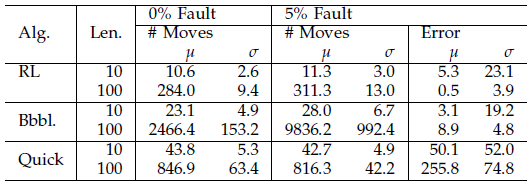
表一汇总列出了三种算法的排序性能。其中,RL 排序算法对数组的更改最小。这是由于 RL 排序算法并未采用传统排序算法的对比方法。算法的主要运算间用于选择需要执行的动作。当存在错误时,RL 排序算法和快排算法的性能并未发生很大的变化(小于两倍的标准偏差)。而冒泡排序更改数组元素的次数则增加了两倍。RL 排序算法尽可能不会犯严重错误,冒泡排序具有额外的处理过程,可以修正错误。但是快排算法一旦给出排序,就不再重新操作结果。
当数组存在错误时,实验中使用错误排序输出与正确排序输出间的欧氏距离衡量错误的大小。距离为零,表明算法返回了正确排序的数组。距离较大,表明算法结果与正确排序间存在较大的偏差。虽然相似性度量是一种衡量错误大小的理想特征向量,但是在正确排序数组未知的情况下,是不可能计算得到相似度的。在论文的实验中,作者考虑注入 5% 的错误率。结果表明,RL 排序算法的错误大小保持恒定,随数组规模发生较小变化,而标准偏差相对较高。冒泡排序具有同等的错误大学,但是对数组的更改次数则高出了数个量级。快排算法给出了数个量级高的错误大小。很明显,RL 排序算法对噪声具有韧性,并且更改数组的次数也是最少的。在更多数据集上的实验结果,参见论文原文附表。
表一 排序特性列表。表中显示了随机初始聚类、数组长度和噪声对排序的影响。对比试验平均执行 100 次,测量数组数值元素位置改变的次数。
图一可视化地展示了在未引入错误条件下,RL 排序、快排和冒泡排序这三种算法在实现排序运算过程中数组的变化情况。三种算法分别需要执行 111(图 1a)、433(图 1b)和 608 步(图 1c)。冒泡排序算法对数组每次更改的范围较小,快排算法围绕锚点元素周围做大范围的元素移动。RL 排序算法(图 1a)利用了数据中的结构,将数组渐进地排序为逐渐增大的子数组。这是因为智能体在每一步都会降低近邻无序元素的数量。因此,RL 排序需要最少的数组操作。图 1d、图 1f 分别显示了同一数组在不可靠比较情况下的排序情况。当存在不可靠比较的情况下,RL 排序由于错误信息采用了不同的轨迹到达目标状态,即正确排序的数组。不正确信息影响了排序算法的本地选取,但由于算法的决策仅考虑本地信息,因此不影响给出正确排序的数组。而快排算法因为不再访问算法已排序的部分数组,因此会产生失败。这解释了表一中的高错误率的原因。
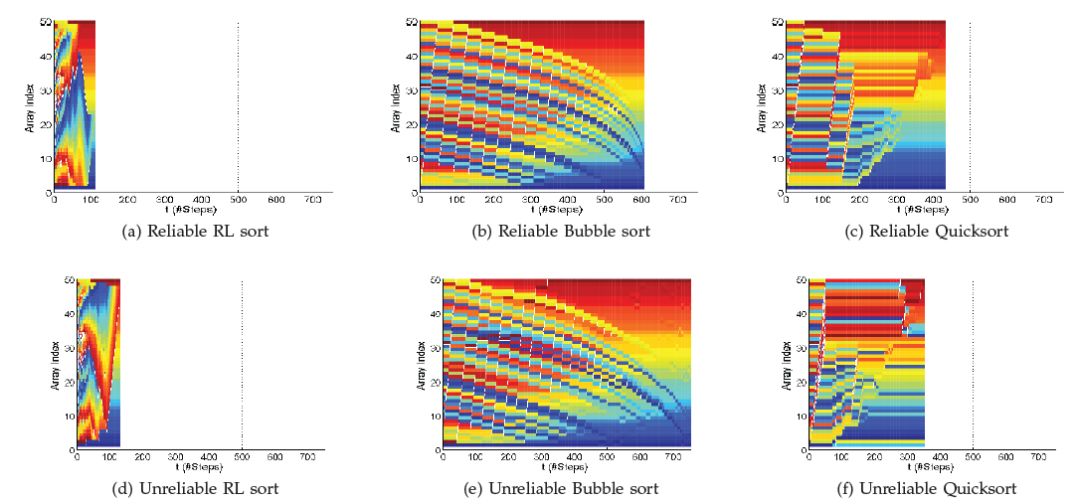
图一 三种算法对具有 50 个元素的数组的排序过程。
图二可视化地展示了数组中间结果的变化情况。图 2a 和 2b 给出了另一种查看算法过程的方式。从图 2a 看,RL 排序给出了一种可靠对比单调向排序的过程,表现出了渐进稳定性。冒泡排序和快排算法中存在一些反复的过程,因此并非单调向排序的。图 2b 显示了在存在错误的情况下,RL 排序算法在前期阶段是平稳推进的,后期阶段略有反复情况。而快排算法则会失败,而冒泡排序由于可以重新访问已排序的部分,因此最终也能给出正确的排序结果。
图 2c 和 2d 显示了算法韧性随错误率变化的情况。图 2c 对比显示了成功排序数组的比例随失败概率变化的情况。对于 5% 的失败率,快排完全不可能给出排序结果。冒泡排序在错误率高于 10% 时会完全失败。RL 排序在错误率 50% 以下时,都可能给出正确的排序。这验证了论文提出的理论结果。图 2d 给出了最终错误(即终止状态和排序数组间的欧氏距离)的均值和标准偏差,数值越低越好。RL 排序算法总是能保持最低。快排算法的错误则是一条凸曲线,意味着即便是最小的初始错误,都会导致最终结果存在很大的错误。总而言之,与这些经典排序算法相比,RL 排序算法更有可能实现正确的排序运算。即便产生错误,RL 排序算法给出的结果也是最接近于正确结果的。
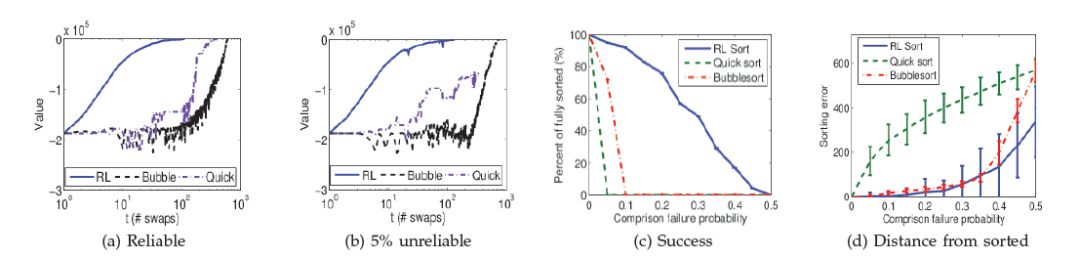
图二 算法韧性随错误率变化的情况
结 论
论文给出了一种稳定和韧性的反馈控制的顺序决策制定理念,解决了存在于传统计算中的对错误的稳定性和终止限制问题。该理念将计算看成是一种轨迹生成问题,应用强化学习方法于实现自治的计算智能体,并使用李雅普诺夫稳定性理论分析。基于此,论文实现了一种稳定、韧性的排序智能体。论文验证了智能体在存在错误情况下的稳定性,以及在存在软件错误情况下维持稳定过程和给出正确结果的概率。
论文提出的韧性计算方法的优点包括:一、对错误源做了尽可能少的假设,具有普适性;二、不需要做手工编程,只需要对问题做形式化定义。智能体的高计算复杂度提高了在不可靠条件下的韧性。在适用于大规模通用计算时,可以通过使用硬件加速和其它一些工程方法降低运算复杂度。
论文在实验中对比了 RL 智能体和两种经典排序算法,进一步验证了理论,并显示了 RL 排序智能体比传统算法在更少操作数据的情况下完成排序。在未来工作中,将进一步开发操作次数具有更紧致上界的 RL 排序算法。
 爱站程序员基地
爱站程序员基地