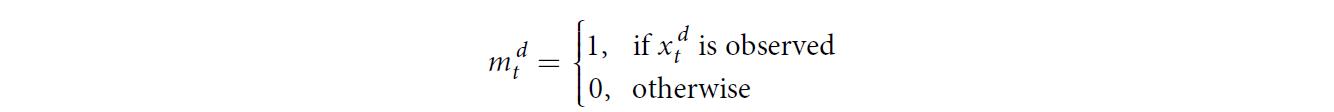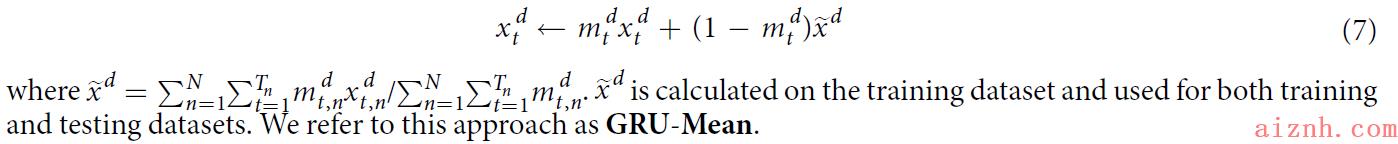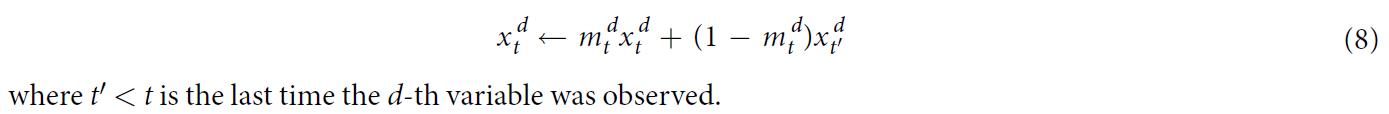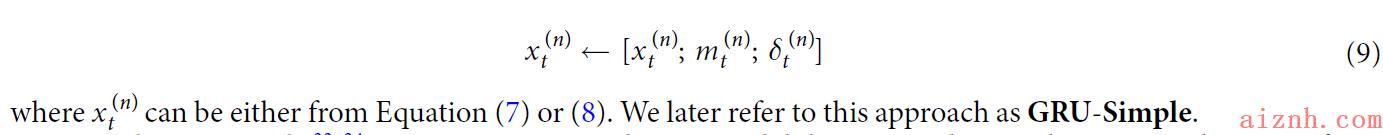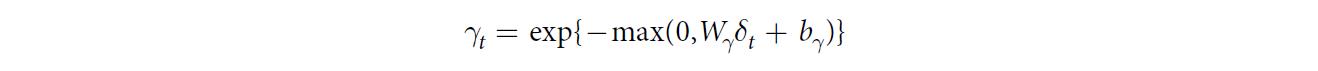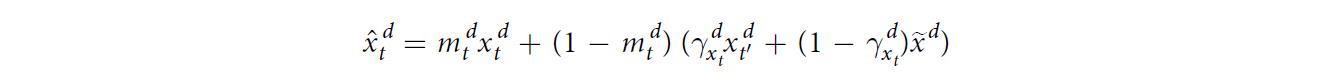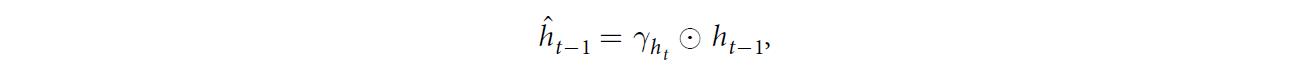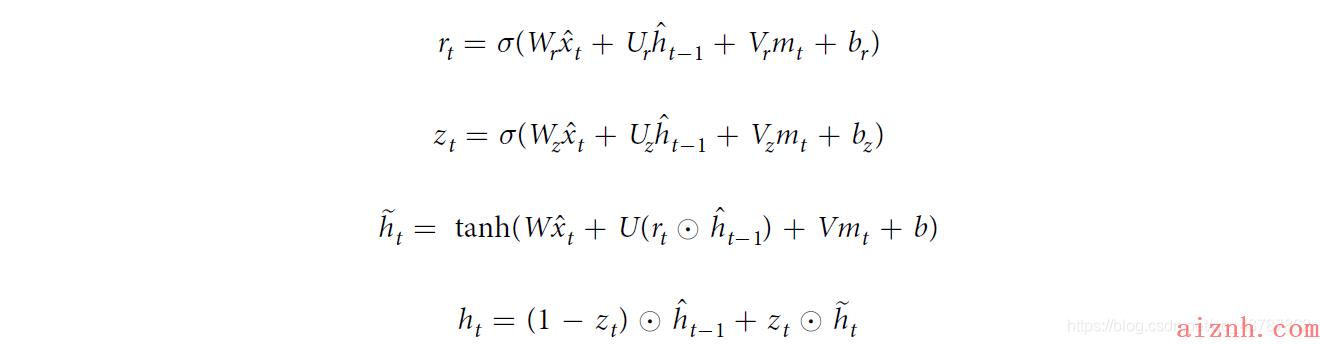这篇文章有附加材料,有比较详尽的数据处理等过程的介绍
0. Title
Multivariate Time Series with Missing Values
1. Research Objective
In this paper, we develop a novel deep learning model based on GRU, namely GRU-D, to effectively exploit two representations of informative missingness patterns, i.e., masking and time interval.
- Masking informs the model which inputs are observed (or missing).
- time interval encapsulates the input observation patterns.
Thus not only capturing the long-term temporal dependencies of time series observations but also utilizing the missing patterns to improve the prediction results
2. Background and Problems
- Multivariate time series data often inevitably carry missing observations due to various reasons which are usually informative missingness.
- Traditional methods dealing with missing values in time series do not capture variable correlations and may not capture complex pattern to perform imputation.
- In other methods, the missing patterns are not effectively explored in the prediction model, thus leading to suboptimal analyses results.
3. Method
Notations
- a msking vector mt∈{0,1}Dm_t \\in \\{0,1\\}^Dmt∈{0,1}D is introduced to denote which variables are missing at time step ttt.
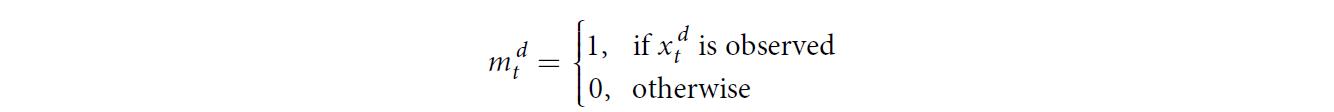
- a time interval δtd∈R\\delta_t^d\\in Rδtd∈R for each variable ddd since its last observation

Model structure

Handling missing values
There are three straightforward ways to handle missing values without applying any imputation approaches or making any modifications to GRU network architecture.
- GRU-Mean:simply to replace each missing observation with the mean of the variable across the training examples.
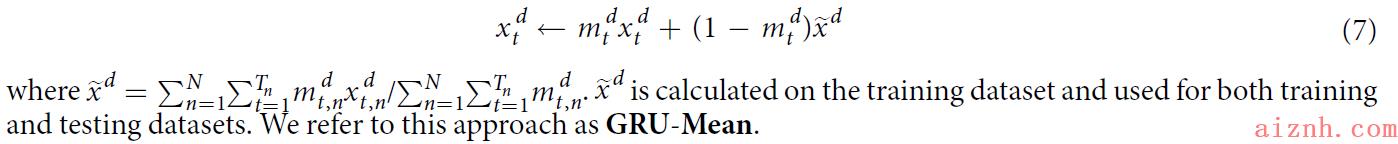
- GRU-Forward:assume any missing value is the same as its last measurement and use forward imputation.
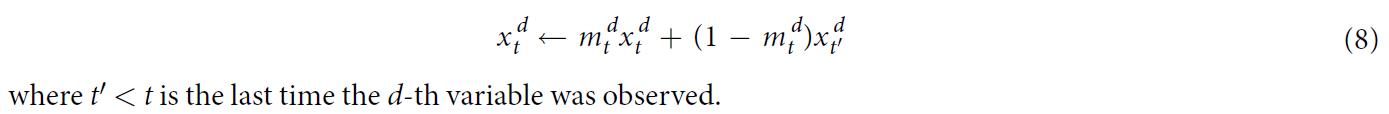
- GRU-Simple:simply indicates which variables are missing and how long they have been missing as a part of input by concatenating the measurement
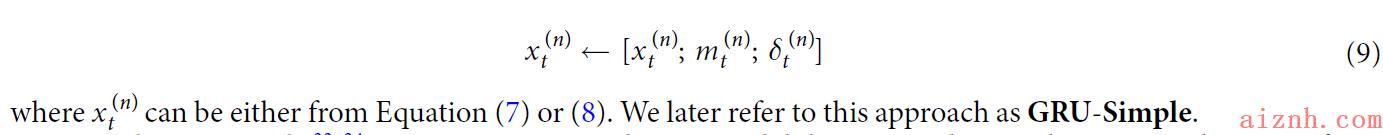
- GRU-Simple w/o mmm(without masking)
- GRU-Simple w/o δδδ(without time interval)
GRU-D: model with trainable decays.
Two properties of the missing values in time series:
- First, the value of the missing variable tend to be close to some default value if its last observation happens a long time ago.
- Second, the influence of the input variables will fade away over time if the variable has been missing for a while.
Therefore, we propose a GRU-based model called GRU-D, in which a decay mechanism is designed for the input variables and the hidden states to capture the aforementioned properties.
A vector of decay rates was introduced for two purpose:
- First, each input variable in health care time series has its own meaning and importance in medical applications. The decay rates should differ from variable to variable based on the underlying properties associated with the variables.
- Second, as we see lots of missing patterns are informative and potentially useful in prediction tasks but unknown and possibly complex, we aim at learning decay rates from the training data rather than fixed a priori.
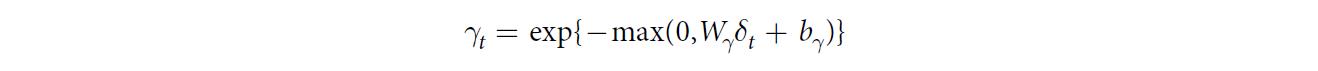
There are two decay mechanisms to utilize the missingness directly with the input feature values and implicitly in the RNN states. - First, for a missing variable, we use an input decay γx\\gamma_xγx to decay it over time toward the empirical mean
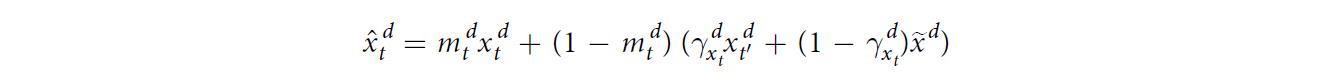
- hidden state decay γh\\gamma_hγh:this has an effect of decaying the extracted features (GRU hidden states) rather than raw input variables directly.
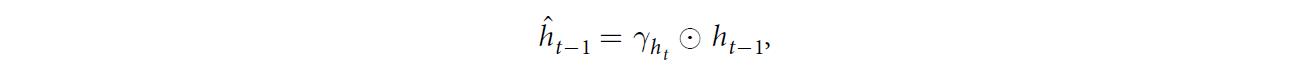
And new model becomes: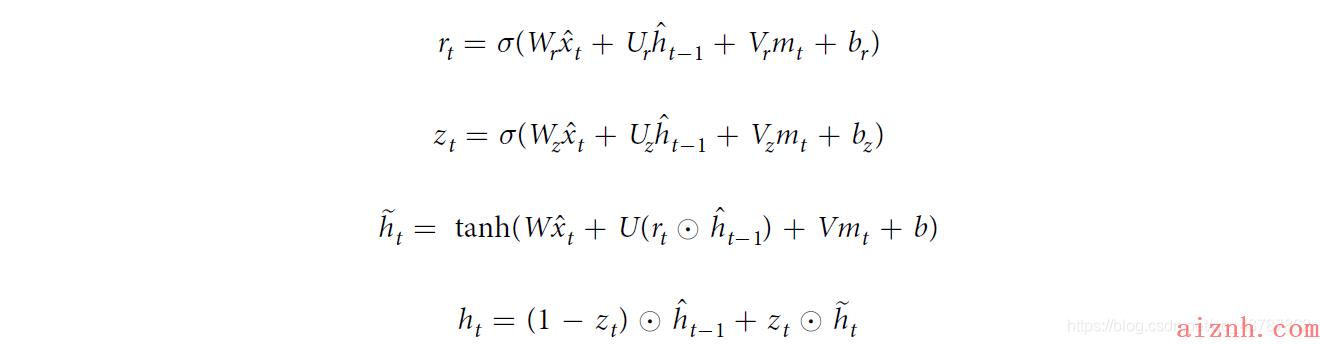
4. Evaluation
5. Conclusion
- These empirical findings validate our assumption that GRU-D utilizes the missing patterns only when the correlations are high and relies on the observed values when the correlations between labels and missing rates are low.
6. Notes
- The author found that the value of missing rate is correlated with the labels, and the missing rate of variables with low missing rate are usually highly (either positive or negative) correlated with the labels which are mortality and ICD-9 diagnosis categories.
 爱站程序员基地
爱站程序员基地