其实在之前的 Inference Variational 那一节中, 我们讲到过一些有关于 Markov Chain Monte Carlo (MCMC) 的知识。也就是我们有一些数据 X，看到这些数据 X，并且有一些隐变量 Z，我们给隐变量一些先验，根据观测数据来推后验知识，也就是 P(Z∣X)P(Z | X)P(Z∣X)
但是，很不幸的是 P(Z∣X)P(Z | X)P(Z∣X) 的计算非常的复杂，我们大致采用两种思路来解决这个问题，也就是 精确推断和近似推断。精确推断无法达到我们想要的结果时，就会采用近似推断的方法。而近似推断中我们又可以分成两大类，即为确定性近似 (VI) 和随机近似 (MCMC)。

Monte Carlo Method 是一种基于采样的随机近似算法。我们的目标是求解后验概率 P(Z∣X),P(Z | X),P(Z∣X), 其中 Z 为 Latent data，X 为 Observed data。知道分布以后，我们通常的目标是求解：
EZ∣X[f(Z)]=∫ZP(Z∣X)f(Z)dZ≈1N∑i=1Nf(zi)\\mathbb{E}_{Z | X}[f(Z)]=\\int_{Z} P(Z | X) f(Z) d Z \\approx \\frac{1}{N} \\sum_{i=1}^{N} f\\left(z_{i}\\right)EZ∣X[f(Z)]=∫ZP(Z∣X)f(Z)dZ≈N1i=1∑Nf(zi)
然后，问题马上就来了，我们知道了后验分布 P(Z∣X),P(Z | X),P(Z∣X), 怎么去采样呢? 也就是如何通过采样得到 z(1),z(2),⋯ ,z(N)∼P(Z∣X)z^{(1)}, z^{(2)}, \\cdots, z^{(N)} \\sim P(Z | X)z(1),z(2),⋯,z(N)∼P(Z∣X) 。那么，我们这一节将要主要介绍三种采样方法，

概率分布采样
拒绝采样
重要性采样

所以，MCMC要解决的问题是

计算复杂积分∫p(x)q(x)q(x)dx\\int \\frac{p(x)}{q(x)} q(x)dx∫q(x)p(x)q(x)dx
求f(x)f(x)f(x)的期望，其中x∼P(x)x \\sim P(x)x∼P(x)
Ep(x)[f(x)]=∫P(x)f(x)dx\\mathbb{E}_{p(x)}[f(x)]=\\int P(x) f(x) d xEp(x)[f(x)]=∫P(x)f(x)dx

MCMC方法描述：
将所需求的式子描述成关于某个分布的期望的形式：Ep(x)[f(x)]\\mathbb{E}_{p(x)}[f(x)]Ep(x)[f(x)]
然后对分布P(x)进行采样，得到x(1),x(2),⋯ ,x(N)∼P(x)x^{(1)}, x^{(2)}, \\cdots, x^{(N)} \\sim P(x)x(1),x(2),⋯,x(N)∼P(x) ,则有
Ep(x)[f(x)]≈1N∑i=1Nf(xi)\\mathbb{E}_{p(x)}[f(x)] \\approx \\frac{1}{N} \\sum_{i=1}^{N} f\\left(x_{i}\\right)Ep(x)[f(x)]≈N1i=1∑Nf(xi)

1 采样方法

1.1概率分布采样

常用写法

c.d.f：概率分布函数（从0到1的函数）
p.d.f ：概率密度函数
i.i.d ：独立同分布

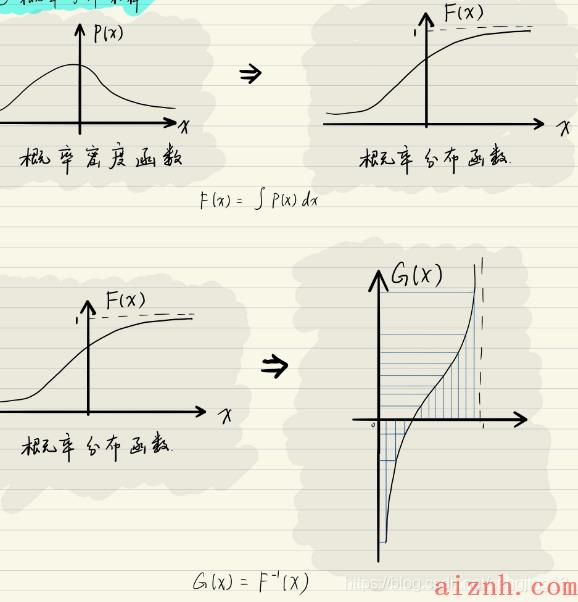
为什么要有概率分布采样呢？因为我们直接根据概率分布来进行采样非常的复杂。如果我们知道概率分布的具体形式吗？我们可以直接求得概率累积的概率分布函数。由于概率分布函数的值一定是 [0,1] 之间的。所以，我们可以在均匀概率密度分布 U(0,1)U(0,1)U(0,1) 上采样, 得到 u(i)∼U(0,1)u^{(i)} \\sim U(0,1)u(i)∼U(0,1) 。然后求 x(i)∼x^{(i)} \\simx(i)∼ cdf−1(u(i))c d f^{-1}\\left(u^{(i)}\\right)cdf−1(u(i)) 就可以计算得到我们想要的结果。这样就可以采样得到 {x(1),x(2),⋯ ,x(N)}N\\left\\{x^{(1)}, x^{(2)}, \\cdots, x^{(N)}\\right\\} \\mathrm{N}{x(1),x(2),⋯,x(N)}N 个样本点。蝠然，理论上这个方法好像很有效，但是实际上很多情况我们都根本不知道 p.d.f 的具体表现形式。就算知道，很多时候 c.d.f 也并不是那么的好求。所以很多情况下，概率分布采样并没有那么的好求。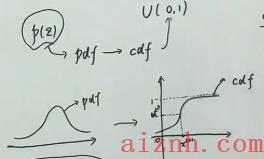

1.2 拒绝采样(Rejection Sampling)

由于对目标分布 p(Z)p(Z)p(Z) 的采样非常的困难，所以我们可以对一个比较筒单的分布 q(Z)q(Z)q(Z) 进行采样来辅助采样。那么我们具体做法怎么办呢？我们可以设定一个 proposal distribution： q(Z)q(Z)q(Z) 。对于 ∀zi,\\forall z_{i},∀zi, 保证 M⋅q(zi)≥p(zi),M \\cdot q\\left(z^{i}\\right) \\geq p\\left(z^{i}\\right),M⋅q(zi)≥p(zi), 那么我们为什么要引入 MMM 呢? 这是因为 ∫ZP(Z)dZ=∫Zq(Z)dZ=1。\\int_{Z} P(Z) d Z=\\int_{Z} q(Z) d Z=1 。∫ZP(Z)dZ=∫Zq(Z)dZ=1。要使 q(zi)≥p(zi)q\\left(z^{i}\\right) \\geq p\\left(z^{i}\\right)q(zi)≥p(zi) 是几乎不可能成立的。
为什么这样做呢？如下图，p(z)是我们需要采样的原始分布，但是通常很难采样，或者说分布不清楚。所以我们可以⽤⼀个提议分布来进⾏采样，主要的思路是如果采样点落在p(z)下⽅，即蓝线下方的阴影部分则接收，反之拒绝。为了方便描述，我们画图来说明一下：

在这里我们需要定义一个接受率： α=P(z(l))M⋅q(z(t)),\\alpha=\\frac{P\\left(z^{(l)}\\right)}{M \\cdot q\\left(z^{(t)}\\right)},α=M⋅q(z(t))P(z(l)), 很显然 0≤α≤10 \\leq \\alpha \\leq 10≤α≤1 。这个实际就是上图中绿色的部分。我们来看看具体的步骤：

(1) 首先进行采样 z(i)∼q(z)z^{(i)} \\sim q(z)z(i)∼q(z)
(2) 计算接受率： α=P(z(i))M⋅q(z(i)),\\alpha=\\frac{P\\left(z^{(i)}\\right)}{M \\cdot q\\left(z^{(i)}\\right)},α=M⋅q(z(i))P(z(i)),
(3) u∼U(0,1)u \\sim U(0,1)u∼U(0,1); 如果 u≤α,u \\leq \\alpha,u≤α, 我们就接收 z(i),z^{(i)},z(i), 不然我们就拒绝。

所以，绿色的部分就被我们称为拒绝区域，就是这样来的，所以这个采样方法就是拒绝采样。同样这样的采样方法也有缺点。如果 M⋅q(z)M \\cdot q(z)M⋅q(z) 比 p(z)p(z)p(z) 大很多的话，那么我们的采样老是是失败的，这就涉及到一个采样效率低下的问题。而当 M⋅q(z)=p(z)M \\cdot q(z)=p(z)M⋅q(z)=p(z) 的时候， α=1,\\alpha=1,α=1, 我们每次采样的结果都是接受的。但是，实际上 p(z)p(z)p(z) 的分布形式非常的复杂，我们根本就没有办法来得到那么准确的结果，特别是采样 cost 非常高的话，经常性的采样失败带来的损失是很大的。

1.3重要性采样(Importance Sampling)

拒绝采样中的接受率过小的时候，被丢弃的样本过多，导致我们得到的有效样本过少。重要性采样就是为了解决拒绝采样样本过少的问题。
重要性采样在我们的强化学习 (PPO) 中的应用非常的多。重要性采样并不是直接对概率进行采样，而是对概率分布的期望进行采样。也就是：
Ep(z)[f(z)]=∫p(z)f(z)dz=∫p(z)q(z)q(z)f(z)dz=∫f(z)p(z)q(z)q(z)dz≈1N∑i=1Nf(zi)p(zi)q(zi)zi∼q(z),i=1,2,⋯ ,N\\begin{aligned}\\mathbb{E}_{p(z)}[f(z)]=\\int p(z) f(z) d z=& \\int \\frac{p(z)}{q(z)} q(z) f(z) d z \\\\=& \\int f(z) \\frac{p(z)}{q(z)} q(z) d z \\\\\\approx & \\frac{1}{N} \\sum_{i=1}^{N} f\\left(z_{i}\\right) \\frac{p\\left(z_{i}\\right)}{q\\left(z_{i}\\right)} \\\\& z_{i} \\sim q(z), i=1,2, \\cdots, N\\end{aligned}Ep(z)[f(z)]=∫p(z)f(z)dz==≈∫q(z)p(z)q(z)f(z)dz∫f(z)q(z)p(z)q(z)dzN1i=1∑Nf(zi)q(zi)p(zi)zi∼q(z),i=1,2,⋯,N
而这里的 p(zt)q(zt)\\frac{p\\left(z_{t}\\right)}{q\\left(z_{t}\\right)}q(zt)p(zt) 也就是 Weight，用来平衡不同的柳率密度值之间的差距。同样重要性采样也可能会出现一些问题，就是两个分布之间的差距太大了话，总是采样采不到重要的样本，采的可能都是实际分布概率值小的部分。也就是采样效率不均匀的问题。在这个基础上，我们进一步提出了Sampling Importance Resampling。

1.4 重要性重采样(Sampling Importance Resampling)

经过重要性采样后，我们得到了N 个样本点，以及对应的权重。那么我用权重来作为采样的概率，
重新测采样出N 个样本。也就是如下图所示：

通过二次采样可以降低采样不平衡的问题。至于为什么呢？大家想一想，我在这里表达一下自己
的看法。p(zt)q(zt)\\frac{p\\left(z_{t}\\right)}{q\\left(z_{t}\\right)}q(zt)p(zt)是Weight，如果Weight 比较大的话，说明p(zi)p(z_i)p(zi) 比较大而q(zi)q(z_i)q(zi) 比较的小，也就是我
们通过q(zi)q(z_i)q(zi) 采出来的数量比较少。那么我们按权重再来采一次，就可以增加采到重要性样本的概率，成功的弥补了重要性采样带来的缺陷，有效的弥补采样不均衡的问题。

2 Markov Chain

在上一小节中，我们描述了三种采样方法，

概率分布采样
拒绝采样法
重要性采样法。

这三种采样方法在高维情况下的采样效率很低，所以我们需要另找方法。

2.1 基础概念介绍

首先我们要明确什么是Random Process，也就是它研究的变量是一个随机变量的序列{xtx_txt}。通
俗的说就是，随机过程就是一个序列，而这个序列中的每一个元素都是一个随机变量。

而Markov Chain 就是一个特殊的随机过程，它的时间和状态都是离散的。并且，Markov Chain
需要满足Markov 性质，也就是未来和过去是无关的。我们用数学的语言表达就是：
P(xt+1=x∣x1,x2,⋯ ,xt)=P(xt+1∣x1,x2,⋯ ,xt−m)P\\left(x_{t+1}=x | x_{1}, x_{2}, \\cdots, x_{t}\\right)=P\\left(x_{t+1} | x_{1}, x_{2}, \\cdots, x_{t-m}\\right)P(xt+1=x∣x1,x2,⋯,xt)=P(xt+1∣x1,x2,⋯,xt−m)
上述公式就是一个 m 阶马尔可夫性质。
齐次 (一阶) 马尔可夫假设：第t+1t+1t+1时刻xxx的状态仅与第ttt时刻xxx的状态有关，即

P(xt+1=x∣x1,x2,⋯ ,xt)=P(xt+1∣xt)P\\left(x_{t+1}=x | x_{1}, x_{2}, \\cdots, x_{t}\\right)=P\\left(x_{t+1} | x_{t}\\right)P(xt+1=x∣x1,x2,⋯,xt)=P(xt+1∣xt)
而 P(xt+1∣xt)P\\left(x_{t+1} | x_{t}\\right)P(xt+1∣xt) 这个概率我们用什么来表达呢?我们定义ア为一个转移矩阵 [Pij],[P_{i j}],[Pij], 而 Pij=P(xt+1=j∣xt=i)P_{i j}=P(x_{t+1}=j | x_{t}=i)Pij=P(xt+1=j∣xt=i)

马氏链定理

有上边的例⼦可以看到，⽆论初始状态是什么，只要转移状态矩阵确定了之后，在经过⽆数次的转移之后，每个点的概
率都会保持不变，⽽最终的这个分布概率就是平稳分布。

2.2 平稳分布(Stationary Distribution)

一个Markov Chain 可以用下图来表示：

此图就是一个时间序列，xix_ixi就表示在第i 时刻的状态，而每一个状态都是一个随机变量。而πi\\pi_iπi 描述的就是第iii 个随机变量的分布。对于一个马氏链来讲，它在第t+1t+1t+1 时刻的概率分布，可以被我们表达为：
πt+1(x∗)=∫πt(x)⋅P(x↦x∗)dx\\pi_{t+1}\\left(x^{*}\\right)=\\int \\pi_{t}(x) \\cdot P\\left(x \\mapsto x^{*}\\right) d xπt+1(x∗)=∫πt(x)⋅P(x↦x∗)dx
熟悉强化学习的同学就会觉得这个公式非常的熟悉。通俗的讲，他实际上就是所有可能转移到状态 xt+1x_{t+1}xt+1 的概率分布的和。那么什么是随机分布呢?
假如这里存在一个 π,\\pi,π, 这里的 π\\piπ 和前面的 πt\\pi_{t}πt 和 πt+1\\pi_{t+1}πt+1 都没有一毛钱关系。假如 π\\piπ 是一个概率分布，那么它可以被我们写成一个无限维向量的形式：
π=[π(1),π(2),⋯ ,π(t),⋯ ],∑i=1∞π(i)=1\\pi=[\\pi(1), \\pi(2), \\cdots, \\pi(t), \\cdots], \\quad \\sum_{i=1}^{\\infty} \\pi(i)=1π=[π(1),π(2),⋯,π(t),⋯],i=1∑∞π(i)=1
如果存在上面的公式使得使得下式成立：
π(x∗)=∫π(x)⋅P(x↦x∗)dx\\pi\\left(x^{*}\\right)=\\int \\pi(x) \\cdot P\\left(x \\mapsto x^{*}\\right) d xπ(x∗)=∫π(x)⋅P(x↦x∗)dx
我们就称 {π(k)}k=1∞\\{\\pi(k)\\}_{k=1}^{\\infty}{π(k)}k=1∞ 是马氏链 {xk}\\left\\{x_{k}\\right\\}{xk} 的平稳分布。看了数学的描述我相信大部分同学还是不懂这个平稳分布时是个什么东西？用通俗的话讲就是，对于一个马氏链来说，每个时刻都符合一个概率分布，如果每一个时刻的概率的分布都是一样的都是 π(k),\\pi(k),π(k), 那么我们就可以称这个马氏链满足一个平稳分布。
那么下一个问题就是我们为什么要引入平稳分布呢？其实，我们想要去求的这个 P(Z)，可以被我们看成是一个平稳分布 π(k),\\pi(k),π(k), 那么我们就可以通过构建一系列的 {x1,x2,⋯ ,xt,⋯ }\\left\\{x_{1}, x_{2}, \\cdots, x_{t}, \\cdots\\right\\}{x1,x2,⋯,xt,⋯} 的马氏链，让它来逼近这个平稳分布。那么我们构建这样的一个马氏链，包括随机变量和转移矩阵，如果它满足平稳分布的条件，确实是可以收剑到平稳分布的。那么，就可以让构建出来的这个马氏链收敘到平稳分布来求得 P(Z)P(Z)P(Z)

题然，已经知道了什么是平稳分布了，那么下一个问题就是，我们需要知道什么样的分布可以称为平稳分布，也就是我们怎样才能构建出一个马氏链让它收敘到一个平稳分布。这里我们需要引入一个条件，也就是 Detailed Balance（平衡分布）：
π(x)⋅P(x↦x∗)=π(x∗)⋅P(x∗↦x)\\pi(x) \\cdot P\\left(x \\mapsto x^{*}\\right)=\\pi\\left(x^{*}\\right) \\cdot P\\left(x^{*} \\mapsto x\\right)π(x)⋅P(x↦x∗)=π(x∗)⋅P(x∗↦x)
大家直观的来想想这个公式，为件么满足它就满足了是一个平稳分布呢？其实并不难想到，对于任意两个状态之间，使用概率分布称为转移概率得到的结果都是可逆的，那么这两个状态之间的分布一定是一样的。而说如果一个分布，满足 Detailed Balance 那么它一定可以是一个平稳分布，但是反过来并不能成立。而证明过程也不难，如下所示：
∫π(x)⋅P(x↦x∗)dx=∫π(x∗)⋅P(x∗↦x)dx=π(x∗)∫P(x∗↦x)⏟∑j=1∞Pij=1dx=π(x∗)\\begin{aligned}\\int \\pi(x) \\cdot P\\left(x \\mapsto x^{*}\\right) d x &=\\int \\pi\\left(x^{*}\\right) \\cdot P\\left(x^{*} \\mapsto x\\right) d x \\\\&=\\pi\\left(x^{*}\\right) \\underbrace{\\int P\\left(x^{*} \\mapsto x\\right)}_{\\sum_{j=1}^{\\infty} P_{i j}=1} d x \\\\&=\\pi\\left(x^{*}\\right)\\end{aligned}∫π(x)⋅P(x↦x∗)dx=∫π(x∗)⋅P(x∗↦x)dx=π(x∗)∑j=1∞Pij=1∫P(x∗↦x)dx=π(x∗)
也就是πP=π\\pi P =\\piπP=π，乘上转移矩阵没有变化。
这样的话，我们就可以不用从定义上来证明一个随机过程是马尔可夫链，直接看它满不满足 Detailed Balance 就可以了。而且这个公式中， π\\piπ 是平稳分布， P(x↦x∗)P\\left(x \\mapsto x^{*}\\right)P(x↦x∗) 是马尔可夫链的状态转移概率, 这样就成功的将平稳分布和马尔可夫链结合在了一起。

综上，MCMC采样的思想：对于我们希望采样的分布P(x)P(x)P(x)，如果我们能找到一个转移矩阵p∗p^{*}p∗，使得p∗p^{*}p∗作为转移矩阵的马氏链的最终的平稳分布为P(x)P(x)P(x)，那么我们就可以通过对马氏链进行采样得到一组样本X∼P(x)X \\sim P(x)X∼P(x)。由于直接构造转移矩阵p∗p^{*}p∗是困难的，所以通过构造满足细致平稳条件的转移矩阵来进行采样。

3 MH采样（Metropolis Hastings Sampling）

上一节中我们讲解了 Detailed Balance，这是平稳分布的充分必要条件。Detailed Balance 为：
π(x)P(x↦x∗)=π(x∗)P(x∗↦x)\\pi(x) P\\left(x \\mapsto x^{*}\\right)=\\pi\\left(x^{*}\\right) P\\left(x^{*} \\mapsto x\\right)π(x)P(x↦x∗)=π(x∗)P(x∗↦x)
这里的 P(x↦x∗)P\\left(x \\mapsto x^{*}\\right)P(x↦x∗) 实际上就是条件概率 P(z∗∣x∗),P\\left(z^{*} | x^{*}\\right),P(z∗∣x∗), 这样写只是便于理解。首先，我们需要明确一点，我们想要求的是后验概率分布 P(Z)，也就是我们推断问题的核心目核。我们求 P(Z) 主要是为了求在 P(Z) 概率分布下的一个相关函数的期望，也就是：
EP(Z)[f(Z)]≈1N∑i=1Nf(z(i))\\mathbb{E}_{P(Z)}[f(Z)] \\approx \\frac{1}{N} \\sum_{i=1}^{N} f\\left(z^{(i)}\\right)EP(Z)[f(Z)]≈N1i=1∑Nf(z(i))
而我们是通过采样来得到 P(Z)∼{z(1),z(2),⋯ ,z(N)}P(Z) \\sim\\left\\{z^{(1)}, z^{(2)}, \\cdots, z^{(N)}\\right\\}P(Z)∼{z(1),z(2),⋯,z(N)} 样本点。 π(x)\\pi(x)π(x) 是最终的平稳分布，可以看成我们这里的 P(Z)，下面的问题就是求出概率转移矩阵 Pij,P_{i j},Pij, 才能满足 Detailed Balance 条件。知道了上面的条件以后，我们每次这样进行采样， x1∼P(x∣x1),x2∼P(x∣x1),x3∼P(x∣x2),⋯ ,xNx_{1} \\sim P\\left(x | x_{1}\\right), x_{2} \\sim P\\left(x | x_{1}\\right), x_{3} \\sim P\\left(x | x_{2}\\right), \\cdots, x_{N}x1∼P(x∣x1),x2∼P(x∣x1),x3∼P(x∣x2),⋯,xN，最终就可以得到我们想要的 N 个样本。

3.1 Proposal Matrix

那我们怎么来找这个状态转移矩阵 PijP_{i j}Pij 呢？首先我们可以随机一个状态转移矩阵 QijQ_{i j}Qij ，也就是 Proposal Matrix 那么肯定是：
P(Z)Q(Z∗→Z)≠P(Z∗)Q(Z→Z∗)P(Z) Q\\left(Z^{*}\\to Z\\right) \\neq P\\left(Z^{*}\\right) Q\\left(Z \\to Z^{*}\\right)P(Z)Q(Z∗→Z)=P(Z∗)Q(Z→Z∗)
那么我们就要想办法找到 QijQ_{i j}Qij 使得：
P(Z)Q(Z∗→Z)=P(Z∗)Q(Z→Z∗)P(Z) Q\\left(Z^{*} \\to Z\\right)=P\\left(Z^{*}\\right) Q\\left(Z \\to Z^{*}\\right)P(Z)Q(Z∗→Z)=P(Z∗)Q(Z→Z∗)
注意，Q(Z→Z∗)Q\\left(Z \\to Z^{*}\\right)Q(Z→Z∗)实际上就是条件概率Q(Z∣Z∗)Q\\left(Z | Z^{*}\\right)Q(Z∣Z∗)，二者是一样的。

那么，我们怎么来解决这个问题呢？我们可以在左右两边乘上一个因子来解决这个问题。也就是,
P(Z)Q(Z∗→Z)α(Z∗,Z)⏟P(Z↦Z∗)=P(Z∗)Q(Z→Z∗)α(Z,Z∗)⏟P(Z∗↦Z)P(Z) \\underbrace{Q\\left(Z^{*} \\to Z\\right) \\alpha\\left(Z^{*}, Z\\right)}_{P\\left(Z \\mapsto Z^{*}\\right)}=P\\left(Z^{*}\\right) \\underbrace{Q\\left(Z \\to Z^{*}\\right) \\alpha\\left(Z, Z^{*}\\right)}_{P\\left(Z^{*} \\mapsto Z\\right)}P(Z)P(Z↦Z∗)Q(Z∗→Z)α(Z∗,Z)=P(Z∗)P(Z∗↦Z)Q(Z→Z∗)α(Z,Z∗)
而 α(z,z∗)\\alpha\\left(z, z^{*}\\right)α(z,z∗) 定义为接收率，大小为：
α(z,z∗)=min⁡(1,P(Z∗)Q(Z→Z∗)P(Z)Q(Z∗→Z))\\alpha\\left(z, z^{*}\\right)=\\min \\left(1, \\frac{P\\left(Z^{*}\\right) Q\\left(Z\\to Z^{*}\\right)}{P(Z) Q\\left(Z^{*}\\to Z\\right)}\\right)α(z,z∗)=min(1,P(Z)Q(Z∗→Z)P(Z∗)Q(Z→Z∗))

这样定义就行了？就可以满足 Detailed Balance 吗？我们可以证明一下,
P(Z)Q(Z∗→Z)α(Z,Z∗)=P(Z)Q(Z∗→Z)min⁡(1,P(Z∗)Q(Z→Z∗)P(Z)Q(Z∗→Z))=min⁡(P(Z)Q(Z∗→Z),P(Z∗)Q(Z→Z∗))=P(Z∗)Q(Z→Z∗)min⁡(P(Z)Q(Z∗→Z)P(Z∗)Q(Z→Z∗),1)=P(Z∗)Q(Z→Z∗)α(Z∗,Z)\\begin{aligned}P(Z) Q\\left(Z^{*} \\to Z\\right) \\alpha\\left(Z, Z^{*}\\right) &=P(Z) Q\\left(Z^{*} \\to Z\\right) \\min \\left(1, \\frac{P\\left(Z^{*}\\right) Q\\left(Z \\to Z^{*}\\right)}{P(Z) Q\\left(Z^{*} \\to Z\\right)}\\right) \\\\&=\\min \\left(P(Z) Q\\left(Z^{*} \\to Z\\right), P\\left(Z^{*}\\right) Q\\left(Z\\to Z^{*}\\right)\\right) \\\\&=P\\left(Z^{*}\\right) Q\\left(Z \\to Z^{*}\\right) \\min \\left(\\frac{P(Z) Q\\left(Z^{*}\\to Z\\right)}{P\\left(Z^{*}\\right) Q\\left(Z \\to Z^{*}\\right)}, 1\\right) \\\\&=P\\left(Z^{*}\\right) Q\\left(Z\\to Z^{*}\\right) \\alpha\\left(Z^{*}, Z\\right)\\end{aligned}P(Z)Q(Z∗→Z)α(Z,Z∗)=P(Z)Q(Z∗→Z)min(1,P(Z)Q(Z∗→Z)P(Z∗)Q(Z→Z∗))=min(P(Z)Q(Z∗→Z),P(Z∗)Q(Z→Z∗))=P(Z∗)Q(Z→Z∗)min(P(Z∗)Q(Z→Z∗)P(Z)Q(Z∗→Z),1)=P(Z∗)Q(Z→Z∗)α(Z∗,Z)
那么我们就成功的证明了：
P(Z)Q(Z∗→Z)α(Z∗,Z)⏟P(Z↦Z∗)=P(Z∗)Q(Z→Z∗)α(Z,Z∗)⏟P(Z∗↦Z)P(Z) \\underbrace{Q\\left(Z^{*}\\to Z\\right) \\alpha\\left(Z^{*}, Z\\right)}_{P\\left(Z \\mapsto Z^{*}\\right)}=P\\left(Z^{*}\\right) \\underbrace{Q\\left(Z \\to Z^{*}\\right) \\alpha\\left(Z, Z^{*}\\right)}_{P\\left(Z^{*} \\mapsto Z\\right)}P(Z)P(Z↦Z∗)Q(Z∗→Z)α(Z∗,Z)=P(Z∗)P(Z∗↦Z)Q(Z→Z∗)α(Z,Z∗)
所以，P(Z) 在转移矩阵 Q(Z∣Z∗)α(Z∗,Z)Q\\left(Z | Z^{*}\\right) \\alpha\\left(Z^{*}, Z\\right)Q(Z∣Z∗)α(Z∗,Z) 下是一个平稳分布，也就是一个马尔可夫链，通过在这个马尔可夫链中采样就可以得到我们的相应的数据样本点了。实际上这就是大名鼎鼎的 Metropolis-Hastings 采样法。

3.2 Metropolis-Hastings Sampling

第一步，我们从一个均匀分布中进行采样， u∼U(0,1)u \\sim U(0,1)u∼U(0,1)
第二步，从 Q(Z∣Z(i−1))Q\\left(Z | Z^{(i-1)}\\right)Q(Z∣Z(i−1)) 中进行采样得到样本点 Z∗Z^{*}Z∗
第三步，计算接受率， α=min⁡(1,P(Z∗)Q(Z∣Z∗)P(Z)Q(Z∗∣Z))\\alpha=\\min \\left(1, \\frac{P\\left(Z^{*}\\right) Q\\left(Z | Z^{*}\\right)}{P(Z) Q\\left(Z^{*} | Z\\right)}\\right)α=min(1,P(Z)Q(Z∗∣Z)P(Z∗)Q(Z∣Z∗)) 。注意, 这里的 P(Z)=P^(Z)ZpP(Z)=\\frac{\\hat{P}(Z)}{Z_{p}}P(Z)=ZpP^(Z) 。其中 ZpZ_{p}Zp 指的是归一化因子，几乎非常难以计算，所以一般是未知的。而 P^(Z)=\\hat{P}(Z)=P^(Z)= likelihood ×\\times× prior。所以这里的 P(Z)P(Z)P(Z)和 P(Z∗)P\\left(Z^{*}\\right)P(Z∗) 就是 P^(Z)\\hat{P}(Z)P^(Z) 和P^(Z∗)\\hat{P}\\left(Z^{*}\\right)P^(Z∗) 。由于归一化因子被抵消了，干脆就直.接写成了 P(Z)P(Z)P(Z) 和 P(Z∗)P\\left(Z^{*}\\right)P(Z∗)
第四步，如果 u≤αu \\leq \\alphau≤α 时 Zi=Z∗,Z^{i}=Z^{*},Zi=Z∗, 不然 Zi=Z(i−1)Z^{i}=Z^{(i-1)}Zi=Z(i−1) 这样执行了 N 次，就可以得到 {Z(1),Z(2),⋯ ,Z(N)}\\left\\{Z^{(1)}, Z^{(2)}, \\cdots, Z^{(N)}\\right\\}{Z(1),Z(2),⋯,Z(N)} 个样本点。

3.3 小结

4 Gibbs Sampling（吉布斯采样）

MH采样有两个缺点：

⼀是需要计算接收率。尤其是在特征维度是⾼维空间时，计算量较⼤，并且由于接受率需要计算时间导致收敛时间变⻓。
⼆是有些⾼维数据特征的条件概率分布可能会⽐较好求，但是特征联合分布不好求，

综上两点，因此需要⼀个好的⽅法的改进MH采样。Gibbs 采样⽤于解决⾼维情况下的采样问题。

如果我们要向一个高维的分布 P(Z)=P(Z1,Z2,⋯ ,ZN)P(Z)=P\\left(Z_{1}, Z_{2}, \\cdots, Z_{N}\\right)P(Z)=P(Z1,Z2,⋯,ZN) 中进行采样。那么我们怎么来进行采样呢？我们的思想就是一维一维的来，在对每一维进行采样的时候固定住其他的维度，这就是 GibbsSampling
我们首先规定一个 z−iz_{-i}z−i 是去除 ziz_{i}zi 后的序列， {z1,z2,⋯ ,zi−1,zi+1,⋯ ,zN}\\left\\{z_{1}, z_{2}, \\cdots, z_{i-1}, z_{i+1}, \\cdots, z_{N}\\right\\}{z1,z2,⋯,zi−1,zi+1,⋯,zN}

4.1 A Example

假设 ttt 时刻，我们获得的样本为 z1(t),z2(t),z3(t)z_{1}^{(t)}, z_{2}^{(t)}, z_{3}^{(t)}z1(t),z2(t),z3(t) 那么 t+1t+1t+1 时刻，我们的采样顺序为：
z1(t+1)∼P(z1∣z2(t),z3(t))z2(t+1)∼P(z2∣z1(t+1),z3(t))z3(t+1)∼P(z3∣z1(t+1),z2(t+1))\\begin{array}{l}z_{1}^{(t+1)} \\sim P\\left(z_{1} | z_{2}^{(t)}, z_{3}^{(t)}\\right) \\\\ \\\\z_{2}^{(t+1)} \\sim P\\left(z_{2} | z_{1}^{(t+1)}, z_{3}^{(t)}\\right) \\\\ \\\\z_{3}^{(t+1)} \\sim P\\left(z_{3} | z_{1}^{(t+1)}, z_{2}^{(t+1)}\\right)\\end{array}z1(t+1)∼P(z1∣z2(t),z3(t))z2(t+1)∼P(z2∣z1(t+1),z3(t))z3(t+1)∼P(z3∣z1(t+1),z2(t+1))
从这个例子中，我们应该可以大致理解固定其他的维度然后进行一维一维采样的意思了。而实际上 Gibbs 是一种特殊的 MH 采样，为什么呢？我们来证明一下。

4.2 接受率α\\alphaα的计算

假如我们需要采样的分布P(Z)P(Z)P(Z)中ZZZ是一个多维变量，即Z=(Z1,Z2,⋯ ,Zp)Z=\\left(Z_{1}, Z_{2}, \\cdots, Z_{p}\\right)Z=(Z1,Z2,⋯,Zp)
我们使ZZZ发生转移的时候仅转移其中一个坐标ZiZ_iZi，令转移后的坐标为Zi∗Z_i^*Zi∗，即
Z⇔Z∗ Z \\Leftrightarrow Z^*Z⇔Z∗
(Z1,Z2,⋯ ,Zi,⋯ ,Zp)⇔(Z1,Z2,⋯ ,Zi∗,⋯ ,Zp) \\left(Z_{1}, Z_{2}, \\cdots, Z_i,\\cdots,Z_{p}\\right) \\Leftrightarrow \\left(Z_{1}, Z_{2}, \\cdots, Z_i^*,\\cdots,Z_{p}\\right)(Z1,Z2,⋯,Zi,⋯,Zp)⇔(Z1,Z2,⋯,Zi∗,⋯,Zp)

Z→Zi∗Z\\to Z_i^*Z→Zi∗的转移概率是P(Zi∗∣Z1,Z2,⋯ ,Zi−1,Zi+1,⋯ ,Zp)P\\left(Z_i^*|Z_{1}, Z_{2}, \\cdots, Z_{i-1},Z_{i+1},\\cdots,Z_{p}\\right)P(Zi∗∣Z1,Z2,⋯,Zi−1,Zi+1,⋯,Zp)

Zi∗→ZZ_i^*\\to ZZi∗→Z的转移概率是P(Zi∣Z1,Z2,⋯ ,Zi−1,Zi+1,⋯ ,Zp)P\\left(Z_i|Z_{1}, Z_{2}, \\cdots, Z_{i-1},Z_{i+1},\\cdots,Z_{p}\\right)P(Zi∣Z1,Z2,⋯,Zi−1,Zi+1,⋯,Zp)

则关于P(Z)P(Z)P(Z)的细致平稳条件方程是：

P(Z)P(Zi∗∣Z1,Z2,…Zi−1Zi+1,…Zp)α(Z,Z∗)=P(Z∗)P(Zi∣Z1∗,Z2∗,…,Zi−1∗Zi+1∗,…Zp∗)P(Z) P\\left(Z_{i}^{*} | Z_{1}, Z_{2}, \\ldots Z_{i-1} Z_{i+1}, \\ldots Z_{p}\\right) \\alpha\\left(Z, Z^{*}\\right)=P\\left(Z^{*}\\right) P\\left(Z_{i} | Z_{1}^{*}, Z_{2}^{*}, \\ldots,Z_{i-1}^{*} Z_{i+1}^{*}, \\ldots Z_{p}^{*}\\right)P(Z)P(Zi∗∣Z1,Z2,…Zi−1Zi+1,…Zp)α(Z,Z∗)=P(Z∗)P(Zi∣Z1∗,Z2∗,…,Zi−1∗Zi+1∗,…Zp∗)

令P(Zi∗∣Z1,Z2,…Zi+1,Zi+1,…Zp)=Q(Z,Z∗)P\\left(Z_{i}^{*} | Z_{1}, Z_{2}, \\ldots Z_{i+1}, Z_{i+1,} \\ldots Z_{p}\\right)=Q\\left(Z, Z^{*}\\right)P(Zi∗∣Z1,Z2,…Zi+1,Zi+1,…Zp)=Q(Z,Z∗)

为精简记号，将(Zi∗∣Z1,Z2,…Zi+1,Zi+1,…Zp)\\left(Z_{i}^{*} | Z_{1}, Z_{2}, \\ldots Z_{i+1}, Z_{i+1,} \\ldots Z_{p}\\right)(Zi∗∣Z1,Z2,…Zi+1,Zi+1,…Zp)表示为Z−iZ_{-i}Z−i

Q(Z,Z∗)=P(Zi∗∣Z−i)Q\\left(Z, Z^{*}\\right)=P\\left(Z_{i}^{*} | Z_{-i}\\right)Q(Z,Z∗)=P(Zi∗∣Z−i)

首先回顾一下，MH 采样的方法。我们的目的是从 Q(Z∣Z(t))Q\\left(Z | Z^{(t)}\\right)Q(Z∣Z(t)) 中采样获得 Z∗,Z^{*},Z∗, 然后计算接受率
α=min⁡(1,P(Z∗)Q(Z∣Z∗)P(Z)Q(Z∗∣Z))\\alpha=\\min \\left(1, \\frac{P\\left(Z^{*}\\right) Q\\left(Z | Z^{*}\\right)}{P(Z) Q\\left(Z^{*} | Z\\right)}\\right)α=min(1,P(Z)Q(Z∗∣Z)P(Z∗)Q(Z∣Z∗))
首先我们来看 Q(Z∣Z(t))Q\\left(Z | Z^{(t)}\\right)Q(Z∣Z(t))
Q(Z∣Z(t))=Q(Zi,Z−i∣Zi(t),Z−i(t))Q\\left(Z | Z^{(t)}\\right)=Q\\left(Z_{i}, Z_{-i} | Z_{i}^{(t)}, Z_{-i}^{(t)}\\right)Q(Z∣Z(t))=Q(Zi,Z−i∣Zi(t),Z−i(t))
假设我们现在是在对第 iii 维进行采样, 我们只要关注 P(Zi∗∣Z−i)P\\left(Z_{i}^{*} | Z_{-i}\\right)P(Zi∗∣Z−i) o所以, 我们可以得到 :Q(Z∣Z(t))=: Q\\left(Z | Z^{(t)}\\right)=:Q(Z∣Z(t))= P(Zi∗∣Z−i(t))P\\left(Z_{i}^{*} | Z_{-i}^{(t)}\\right)P(Zi∗∣Z−i(t))
已经成功的将 Q(Z∣Z(t))Q\\left(Z | Z^{(t)}\\right)Q(Z∣Z(t)) 做了等价转换以后。那么我们想要求的 α\\alphaα 可以被我们成功的转换成如下的形式：
α=min⁡(1,P(Zi∗∣Z−i∗)P(Z−i∗)P(Zi∣Z−i∗)P(Zi∣Z−i)P(Z−i)P(Zi∗∣Z−i))\\alpha=\\min \\left(1, \\frac{P\\left(Z_{i}^{*} | Z_{-i}^{*}\\right) P\\left(Z_{-i}^{*}\\right) P\\left(Z_{i} | Z_{-i}^{*}\\right)}{P\\left(Z_{i} | Z_{-i}\\right) P\\left(Z_{-i}\\right) P\\left(Z_{i}^{*} | Z_{-i}\\right)}\\right)α=min(1,P(Zi∣Z−i)P(Z−i)P(Zi∗∣Z−i)P(Zi∗∣Z−i∗)P(Z−i∗)P(Zi∣Z−i∗))

计算到了这里，我们还是不好进行计算，上面和下面好像还是不好消除。如果我们可以得到 Z_-i 和 Z_i 之间的关系就好了。下面我们会得出一个重要的结论来帮助我们计算 α\\alphaα 的具体值。首先我们来举一个例子：

那么假设当 t=1 的时刻，有一个样本为： Z1(1),Z2(1),Z3(1)Z_{1}^{(1)}, Z_{2}^{(1)}, Z_{3}^{(1)}Z1(1),Z2(1),Z3(1)
当 t=2t=2t=2 的时刻，我们假设先对第一维进行采样就可以得到： Z1(2),Z2(1),Z3(1)\\quad Z_{1}^{(2)}, Z_{2}^{(1)}, Z_{3}^{(1)}Z1(2),Z2(1),Z3(1) 很显然 Z2(1),Z3(1)Z_{2}^{(1)}, Z_{3}^{(1)}Z2(1),Z3(1) 根本没有发生变化。我们可以得到 Z−1=Z−1∘∗Z_{-1}=Z_{-1^{\\circ}}^{*}Z−1=Z−1∘∗ 也就是在 Gibbs 采样时，采样前后只关注于一个维度，其他的维度我们都没有关注到。所以就可以得到结论：
Z−i=Z−i∗Z_{-i}=Z_{-i}^{*}Z−i=Z−i∗
那么，我们根据这个结论就可以得到：
α=min⁡(1,P(Zi∗∣Z−i∗)P(Z−i∗)P(Zi∣Z−i∗)P(Zi∣Z−i∗)P(Z−i∗)P(Zi∗∣Z−i∗))=1\\alpha=\\min \\left(1, \\frac{P\\left(Z_{i}^{*} | Z_{-i}^{*}\\right) P\\left(Z_{-i}^{*}\\right) P\\left(Z_{i} | Z_{-i}^{*}\\right)}{P\\left(Z_{i} | Z_{-i}^{*}\\right) P\\left(Z_{-i}^{*}\\right) P\\left(Z_{i}^{*} | Z_{-i}^{*}\\right)}\\right)=1α=min(1,P(Zi∣Z−i∗)P(Z−i∗)P(Zi∗∣Z−i∗)P(Zi∗∣Z−i∗)P(Z−i∗)P(Zi∣Z−i∗))=1
那么计算出接受率为 1，也就是每次都必定被接受。所以，每次从 Q(Z∣Z(t))=P(Zi∗∣Z−i)Q\\left(Z | Z^{(t)}\\right)=P\\left(Z_{i}^{*} | Z_{-i}\\right)Q(Z∣Z(t))=P(Zi∗∣Z−i) 中进行采样得到Zi∗Z_{i}^{*}Zi∗即可，一维一维的进行采样就可以采到整个高维的分布，各个维度上的样本。
所以，解释到了这里，大家基本就可以知道 Gibbs Samplings 是 α=1\\alpha=1α=1 的 MH Sampling 的意义了。在 Gibbs Sampling 中 α=1,\\alpha=1,α=1, 而且状态转移矩阵 Q(Z∣Z(t))=P(Zi∗∣Z−i(t)),Q\\left(Z | Z^{(t)}\\right)=P\\left(Z_{i}^{*} | Z_{-i}^{(t)}\\right),Q(Z∣Z(t))=P(Zi∗∣Z−i(t)), 所以 Gibbs Sampling 就是把目标分布 P 对应的条件概率当作状态转移分布 QQQ。

这里我们需要额外提醒一下，使用 Gibbs Sampling 是有使用前提的，也就是固定其他维度后的一维分布时方便进行采样的，如果固定其他维度的时候得到的一维分布仍然是非常难进行采样的，那么使用 Gibbs Sampling 也是没有用的。

13 MCMC(Markov Chain Monte Carlo)（一）